In 2004, Canadian musician Andrew Huang wrote a song that encodes the first 101 digits of π.
Also: A “piku” is a haiku whose word lengths reflect the digits of π:
How I love a verse
Contrived to unhusk dryly
One image nutshell
In 2004, Canadian musician Andrew Huang wrote a song that encodes the first 101 digits of π.
Also: A “piku” is a haiku whose word lengths reflect the digits of π:
How I love a verse
Contrived to unhusk dryly
One image nutshell
In natural language, the most frequent word occurs about twice as often as the second most frequent word, three times as often as the third most frequent word, and so on.
In the Brown Corpus, a text collection of a million words, the most frequent word, the, accounts for 7.5% of all word occurrences, and the second most frequent, of, accounts for 3.5%. A mere 135 vocabulary items account for half the corpus, and about half the total vocabulary of about 50,000 words are hapax legomena, words that occur once only.
Similar distributions are found in data throughout the physical and social sciences; the law is named after the American linguist George Kingsley Zipf.
A set of points has diameter 1 if no two points in the set are more than 1 unit apart. An example is an equilateral triangle whose side has length 1. What’s the smallest shape that can cover any such set? A circle of diameter 1 won’t cover our triangle; part of the triangle projects beyond the circle:
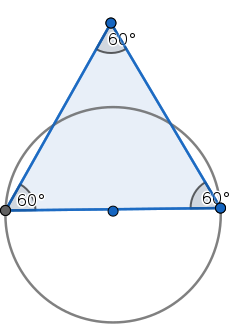
Of course a larger circle would work, but what’s the smallest shape will always do the job? Surprisingly, no one knows. When French mathematician Henri Lebesgue posed the problem to Gyula Pál in 1914, Pál suggested a modified hexagon (in black):
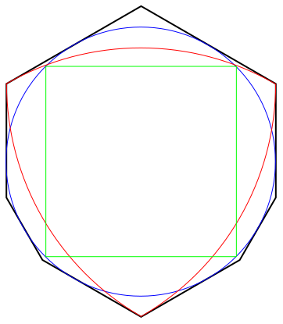
Here Pál’s shape manages to surround a circle (blue), a Reuleaux triangle (red), and a square (green), each of diameter 1, and in fact it will accommodate any such set. Its own area is 0.84529946. Will a smaller shape do the job? Well, yes, but the gains get increasingly fine: In 1936 Roland Sprague whittled Pál’s shape down to 0.844137708436, and in 1992 H.C. Hansen reduced it further to 0.844137708398. At this point observers Victor Klee and Stanley Wagon wrote, “[I]t does seem safe to guess that progress on [this problem], which has been painfully slow in the past, may be even more painfully slow in the future.” But in 2015 John Baez reached 0.8441153 with an exquisite adjustment to two regions in Hansen’s shape; the smaller of these would span only a few atoms if the shape were drawn on paper.
Is that the end of the story? No: Last October Philip Gibbs claimed a further reduction to 0.8440935944, and the search goes on. In 2005 Peter Brass and Mehrbod Sharifi showed that the universal cover must have an area of at least 0.832, so there’s room, at least in theory, for still further improvements.
(Thanks, Jacob.)
In a 2009 study of responses to music, neuroscientist Valorie Salimpoor and her colleagues asked participants to bring in 3 to 5 pieces of “intensely pleasurable instrumental music to which they experience chills.” Then they measured their physiological response as they listened. They found that the “chills” effect is real — when the subjects reported that their pleasure at the music was highest, so was their sympathetic nervous system activity, a measure of emotional arousal.
One byproduct of the study is a list of more than 200 chills-inducing moments in music of various genres, with precise timestamps of the crucial points:
| Composer/Artist | Title | Chills |
| Beethoven | Piano Sonata No. 17 in D Minor (“The Tempest”) | 5:33 |
| Mahler | Symphony No. 1 – Movement 4 | 5:42, 9:57, 15:15 |
| Charles Mingus | Fables of Faubus | 0:20, 7:10 |
| Stan Getz | Round Midnight | 1:26 |
| Pink Floyd | Shine on You Crazy Diamond | 5:00 |
| Phish | You Enjoy Myself | 10:50 |
| Cannonball Adderley | One for Daddy-O | 0:40 |
| Los Angeles Guitar Quartet | Congan | 2:09 |
| Crowfoot | Larks in May | 0:10, 2:00 |
| Howard Shore | The Breaking of the Fellowship (film score) | 0:10, 0:55 |
| Dave Matthews Band | #34 | 1:40 |
| The Dissociatives | Paris Circa 2007 Slash 08 | 1:30 |
| Brad Mehldau | Knives Out | 4:45, 7:25 |
| Explosions in the Sky | First Breath After Coma | 2:25, 3:30, 8:10 |
These won’t work for everyone — music tastes are notoriously idiosyncratic — but it’s interesting to see what people find moving. The full list is here (Table_S1). (Note too that the timestamps relate to a particular recording, so consider them approximate in e.g. classical music.)
(Valorie N. Salimpoor, et al., “The Rewarding Aspects of Music Listening Are Related to Degree of Emotional Arousal,” PloS One 4:10 [2009], e7487.)
While working on his chemistry doctorate in 1947, Isaac Asimov was dissolving catechol in water when it occurred to him that if it were any more soluble it would dissolve before it even touched the surface. Amused by the idea, he invented a fictional substance called thiotimoline, one of whose chemical bonds projects forward into the future and another backward into the past. This makes the chemical “endochronic”: It starts dissolving before it makes contact with water. His first thought was to make this into a science fiction story.
It occurred to me, however, that instead of writing an actual story based on the idea, I might write up a fake research paper on the subject and get a little practice in turgid writing. I did the job on June 8, 1947, even giving it the kind of long-winded title that research papers so often have — ‘The Endochronic Properties of Resublimated Thiotimoline’ — and added tables, graphs, and fake references to non-existent journals.
John W. Campbell of Astounding Science Fiction accepted the article and agreed to publish it under a pseudonym, lest it alienate Asimov’s examiners at Columbia. In the end he published it under Asimov’s own name, but there was no harm done — the examiners joked about it at his defense and it even brought him some fame among chemists. He went on to write three short stories about the substance — which has taken on a rich existence in the hands of other authors.
(Isaac Asimov, “The Endochronic Properties of Resublimated Thiotimoline,” Astounding Science Fiction 41:1 [1948], 120-125. Thanks, Peter.)

What rules underlie natural conversation? In a lecture at Harvard in 1967, British philosopher H.P. Grice set out to specify them using a mathematical approach, as Euclid had done in plane geometry. First, he said, the participants in a conversation follow a Cooperative Principle:
Make your conversational contribution such as is required, at the stage at which it occurs, by the accepted purpose or direction of the talk exchange in which you are engaged.
Then he derived more specific principles under four headings:
These are useful, but they’re not axioms. “[I]t is possible to engage in a genuine and meaningful conversation and yet fail to observe one or more of the maxims Grice listed,” writes Stanford mathematician Keith Devlin. “The maxims seem more a matter of an obligation of some kind.” In Grice’s own words, “I would like to be able to think of the standard type of conversational practice not merely as something which all or most do in fact follow, but as something which it is reasonable for us to follow, which we should not abandon.”
(Keith Devlin, “What Will Count as Mathematics in 2100?”, in Bonnie Gold and Roger A. Simons, eds., Proof & Other Dilemmas: Mathematics and Philosophy, 2008.)
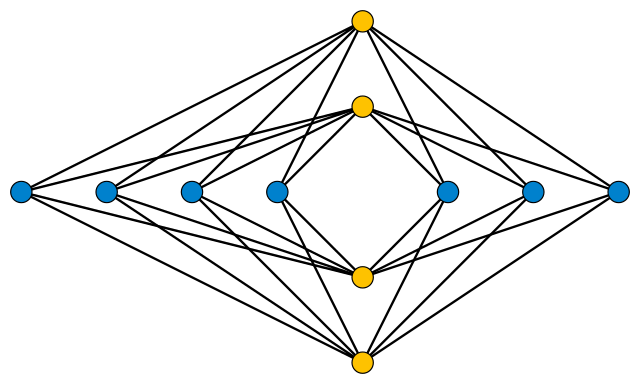
During World War II, Hungarian mathematician Pál Turán was forced to work in a brick factory. His job was to push a wagonload of bricks along a track from a kiln to storage site. The factory contained several kilns and storage sites, with tracks criss-crossing the floor among them. Turán found it difficult to push the wagon across a track crossing, and in his mind he began to consider how the factory might be redesigned to minimize these crossings.
After the war, Turán mentioned the problem in talks in Poland, and mathematicians Kazimierz Zarankiewicz and Kazimierz Urbanik both took it up. They showed that it’s always possible to complete the layout as shown above, with the kilns along one axis and the storage sites along the other, each group arranged as evenly as possible around the origin, with the tracks running as straight lines between each possible pair. The number of crossings, then, is
where m and n are the number of kilns and storage sites and denotes the floor function, which just means that we take the greatest integer less than the value in brackets. In the case of 4 kilns and 7 storage sites, that gives us
which is the number of crossings in the diagram above.
Is that the best we can do? No one knows. Zarankiewicz and Urbanik thought that their formula gave the fewest possible crossings, but their proof was found to be erroneous 11 years later. Whether a factory can be designed whose layout contains fewer crossings remains an open problem.

Today it’s possible to describe a color quantitatively, but how did people make such fine distinctions in the 18th century? German geologist Abraham Gottlob Werner proposed a solution in 1774: His Von den äußerlichen Kennzeichen der Foßilien included a “color dictionary” that located each hue in the natural world. Updated by Scottish painter Patrick Syme, it describes 110 colors, telling where each might be found in animal, vegetable, and mineral form: Number 35, for example, “bluish lilac purple,” is the shade of the male of the dragonfly Libellula depressa, the blue lilac, and the mineral lepidolite. Number 82, “tile red,” may be found in the breast of the cock bullfinch, in the shrubby pimpernel, and in porcelain jasper.
This common language gave naturalists an objective way to communicate what they were seeing. Off Brazil aboard the H.M.S. Beagle in 1832, Charles Darwin wrote, “I had been struck by the beautiful color of the sea when seen through the chinks of a straw hat. It was according to Werner nomenclature ‘Indigo with a little azure blue’. The sky at the time was ‘Berlin [blue] with little Ultra marine’.”
The Internet Archive has Syme’s full text.
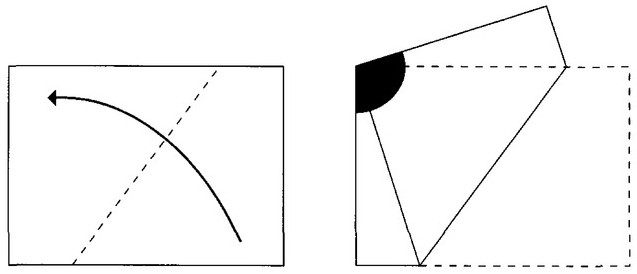
The angle cos-1(-1/3) = 109.47°, familiar from soap films and tetrahedral molecular geometry, can be produced with an ordinary piece of A4 paper: Because it has a width:length ratio of , folding it corner to corner as shown yields a shape with precisely that angle.
(Nick Lord, “A ‘Maths Bite’: How to Impress a Chemist,” Mathematical Gazette 80:489 [1996], 584-584.)

In 1995, NASA astronomer Scott Sandford became troubled by the phrase “You’re comparing apples and oranges.” “First,” he wrote, “the statement that something is like comparing apples and oranges is a kind of analogy itself. That is, denigrating an analogy by accusing it of comparing apples and oranges is, in and of itself, comparing apples and oranges. More importantly, it is not difficult to demonstrate that apples and oranges can, in fact, be compared.”
He desiccated an apple and an orange and ran samples through a spectrometer. “Not only was this comparison easy to make, but it is apparent from the figure that apples and oranges are very similar,” he concluded. “Thus, it would appear that the comparing apples and oranges defense should no longer be considered valid. This is a somewhat startling revelation. It can be anticipated to have a dramatic effect on the strategies used in arguments and discussions in the future.”
Sure enough, five years later surgeon James E. Barone confirmed this result in the British Medical Journal. He found that apples and oranges are both edible, juiceable fruits grown in orchards on flowering trees and subject to damage by disease and insects, and they have comparable color, sweetness, size, shape, and weight. “In only one category, that of ‘involvement of Johnny Appleseed,’ was a statistically significant difference between the two fruits found.”
“This article, certain to become the classic in the field, clearly demonstrates that apples and oranges are not only comparable; indeed they are quite similar,” he concluded. “The admonition ‘Let’s not compare apples with oranges’ should be replaced immediately with a more appropriate expression such as ‘Let’s not compare walnuts with elephants’ or ‘Let’s not compare tumour necrosis factor with linguini.'”