When logician John Venn introduced the famous diagrams that bear his name, he expressed an interest in “symmetrical figures … elegant in themselves.” He thought the “simplest and neatest figure” that showed all possible logical relations among four sets was four equal ellipses arranged like this:

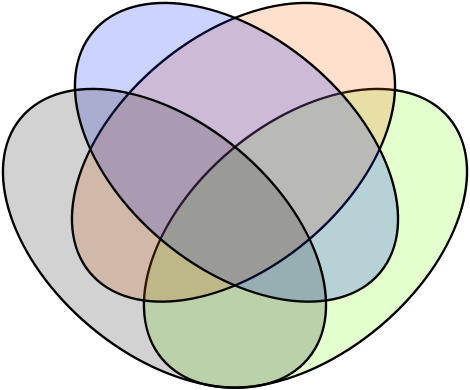
“It is obvious that we thus get the sixteen compartments that we want, counting, as usual, the outside of them all as one compartment. … The desired condition that these sixteen alternatives shall be mutually exclusive and collectively exhaustive, so as to represent all the component elements yielded by the four terms taken positively and negatively, is of course secured.”

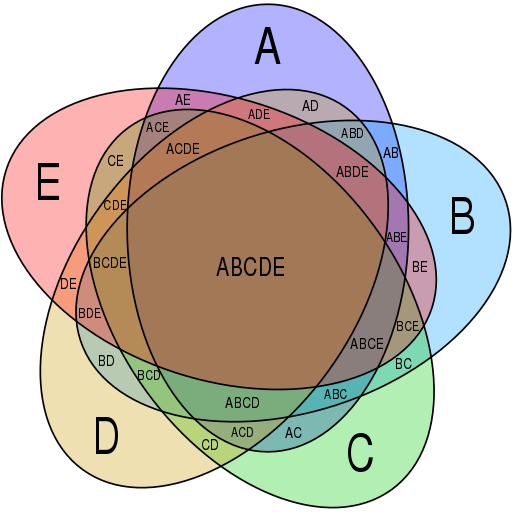
Interestingly, he added that “with five terms combined together ellipses fail us”: Venn believed that it was impossible to create a Venn diagram with five ellipses. Amazingly, that assertion went unchallenged for nearly a century — it was only in 1975 that Branko Grünbaum found a diagram with five ellipses:

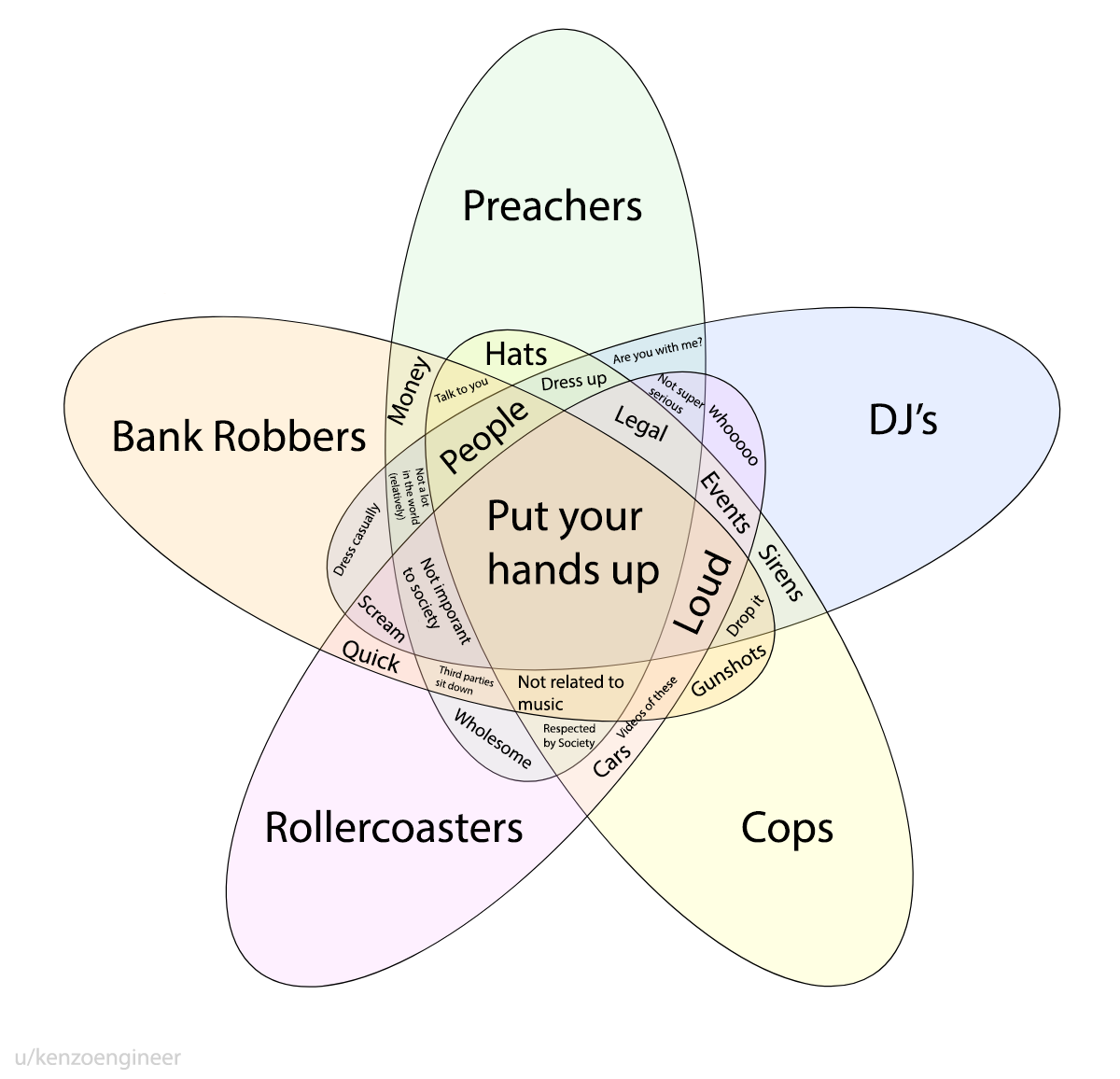
It’s not possible to form a Venn diagram with six or more ellipses. Do we even need one with five? According to Reddit, yes, we do:

(Peter Hamburger and Raymond E. Pippert, “Venn Said It Couldn’t Be Done,” Mathematics Magazine 73:2 [April 2000], 105-110.)