A puzzle by National Security Agency mathematician David B., from the agency’s October 2017 Puzzle Periodical:
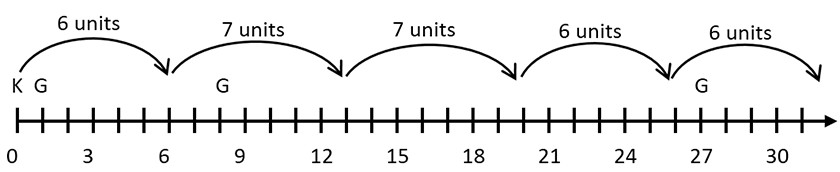
Joey, the baby kangaroo has been kidnapped and placed at 2100 on a number line.
His mother, Kandice the Kangaroo, is at 0 on the number line, and will try to save him. Kandice normally jumps forward 6 units at a time. Guards have been placed at n3 on the number line, for every integer n≥1. If Kandice lands on a number with a guard on it, she will be caught and her mission will fail. Otherwise, she will safely sneak past the guard. Whenever she successfully sneaks past a guard, she gets an adrenaline rush that causes her next jump (the first jump after passing the guard) to take her 1 unit farther than it normally would (7 units instead of 6). (After a single 7-unit jump, she resumes jumping 6 units at a time, until the next time she sneaks past a guard.)
Will Kandice the Kangaroo reach (or pass) her son Joey safely?