Given a group of 10 men and 10 women, all straight, is it always possible to pair them off in stable marriages, that is, to pair them so that there exist no man and woman who would prefer each other to the partners they have? Yes:

• In the first round, each man who’s not yet engaged proposes to the woman he most prefers. Then each woman says “maybe” to the suitor she most prefers and rejects all the others. Now she and the suitor she hasn’t rejected are provisionally engaged.
• In each following round, each man who’s not yet engaged proposes to the woman he most prefers and hasn’t yet approached. He does this even if she’s already engaged. Then each woman says “maybe” to her most preferred suitor, even if that means jilting her current provisional fiancé.

This process continues until everyone is engaged (as they must be, since every man must eventually propose to every woman and every woman must accept someone). All the marriages are stable because no man can end up pining for a woman who would prefer him to her own partner — that woman must already have rejected or jilted him at some point during the courting:

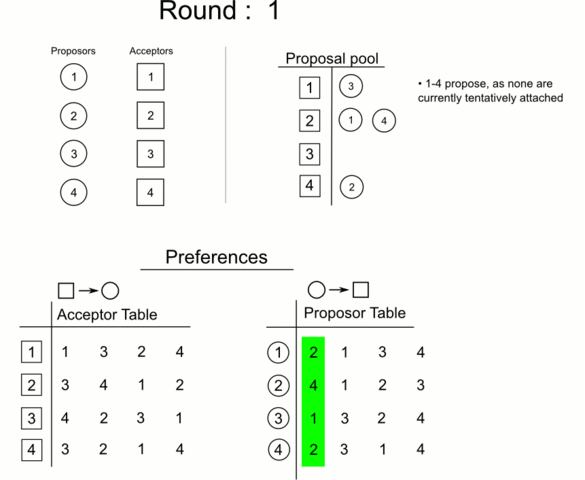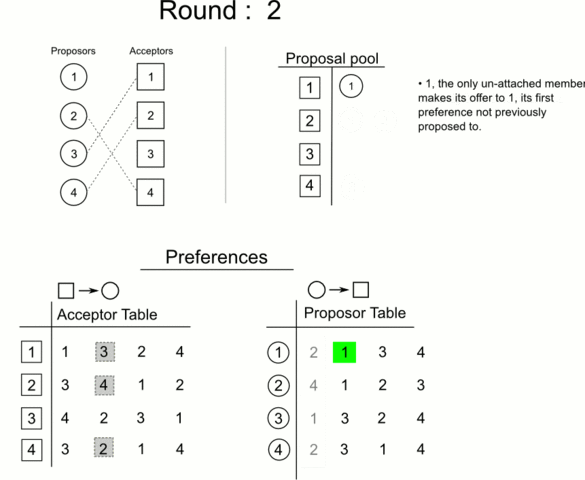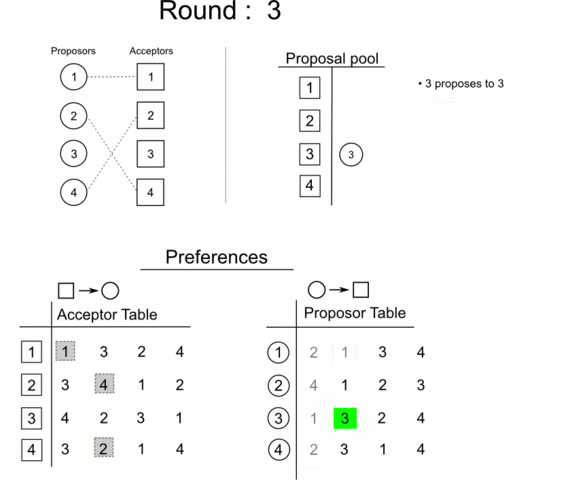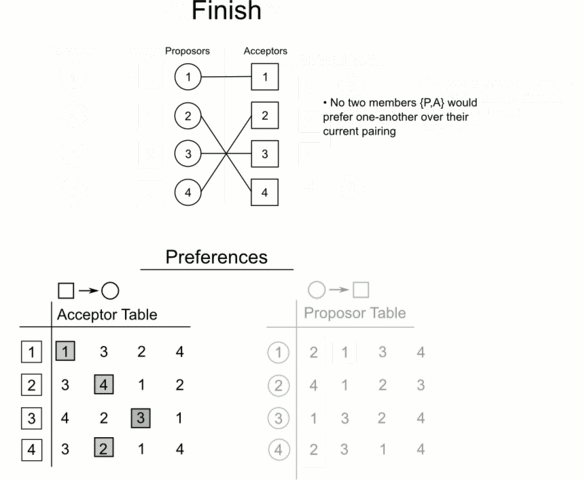
In 1962, mathematicians David Gale and Lloyd Shapley showed that stable marriages can always be found for any equal number of men and women.