
“Climate is your personality; weather is your mood.” — J. Marshall Shepherd, past president, American Meteorological Society, quoted in Andrew Revkin and Lisa Mechaley, Weather: An Illustrated History, 2018

“Climate is your personality; weather is your mood.” — J. Marshall Shepherd, past president, American Meteorological Society, quoted in Andrew Revkin and Lisa Mechaley, Weather: An Illustrated History, 2018
quadragenarian
n. one in her forties
repentine
adj. sudden
monomachy
n. a duel; single combat
labefaction
n. overthrow, downfall
The longest-lived spider on record is Number 16, a wild female trapdoor spider that lived on the North Bungulla Reserve near Tammin, Western Australia. She’d reached age 43 when ecologist Leanda Mason discovered that something, probably a parasitic wasp, had pierced the silk door of her burrow, which was now empty.
“She was cut down in her prime,” Mason told the Washington Post. “It took a while to sink in, to be honest.”
In the 19th century, some New England communities grew so desperate to help victims of tuberculosis that they resorted to a macabre practice: digging up dead relatives and ritually burning their organs. In this week’s episode of the Futility Closet podcast we’ll examine the causes of this bizarre belief and review some unsettling examples.
We’ll also consider some fighting cyclists and puzzle over Freddie Mercury’s stamp.
Two years ago I wrote about the number 84,672, which has a surprising property: When its name is written out in (American) English (EIGHTY FOUR THOUSAND SIX HUNDRED SEVENTY TWO) and the letter counts of those words are multiplied together (6 × 4 × 8 × 3 × 7 × 7 × 3), they yield the original number (84,672).
Such numbers are called fortuitous, and, not surprisingly, very few of them are known. When I wrote about them in 2019, the whole list ran 4, 24, 84672, 1852200, 829785600, 20910597120, 92215733299200. Now Jonathan Pappas has discovered two more:
1,239,789,303,244,800,000
ONE QUINTILLION TWO HUNDRED THIRTY NINE QUADRILLION SEVEN HUNDRED EIGHTY NINE TRILLION THREE HUNDRED THREE BILLION TWO HUNDRED FORTY FOUR MILLION EIGHT HUNDRED THOUSAND
3 × 11 × 3 × 7 × 6 × 4 × 11 × 5 × 7 × 6 × 4 × 8 × 5 × 7 × 5 × 7 × 3 × 7 × 5 × 4 × 7 × 5 × 7 × 8 = 1,239,789,303,244,800,000
887,165,996,513,213,819,259,682,435,576,627,200,000,000
EIGHT HUNDRED EIGHTY SEVEN DUODECILLION ONE HUNDRED SIXTY FIVE UNDECILLION NINE HUNDRED NINETY SIX DECILLION FIVE HUNDRED THIRTEEN NONILLION TWO HUNDRED THIRTEEN OCTILLION EIGHT HUNDRED NINETEEN SEPTILLION TWO HUNDRED FIFTY NINE SEXTILLION SIX HUNDRED EIGHTY TWO QUINTILLION FOUR HUNDRED THIRTY FIVE QUADRILLION FIVE HUNDRED SEVENTY SIX TRILLION SIX HUNDRED TWENTY SEVEN BILLION TWO HUNDRED MILLION
5 × 7 × 6 × 5 × 12 × 3 × 7 × 5 × 4 × 11 × 4 × 7 × 6 × 3 × 9 × 4 × 7 × 8 × 9 × 3 × 7 × 8 × 9 × 5 × 7 × 8 × 10 × 3 × 7 × 5 × 4 × 10 × 3 × 7 × 6 × 3 × 11 × 4 × 7 × 6 × 4 × 11 4 × 7 × 7 × 3 × 8 × 3 × 7 × 6 × 5 × 7 × 3 × 7 × 7 = 887,165,996,513,213,819,259,682,435,576,627,200,000,000
A 10th solution, if one exists, will be greater than 10138.
Details are here. Jonathan has also discovered some cyclic solutions (ONE HUNDRED SIXTY EIGHT -> FIVE HUNDRED TWENTY FIVE -> SIX HUNDRED SEVENTY TWO -> FOUR HUNDRED FORTY ONE -> FOUR HUNDRED TWENTY -> ONE HUNDRED SIXTY EIGHT) and the remarkable 195954154450774917120 -> 195954154450774917120000 -> 1959541544507749171200000.
(Thanks, Jonathan.)
This is pretty: If you choose n > 1 equally spaced points on a unit circle and connect one of them to each of the others, the product of the lengths of these chords equals n.
(Andre P. Mazzoleni and Samuel Shan-Pu Shen, “The Product of Chord Lengths of a Circle,” Mathematics Magazine 68:1 [February 1995], 59-60.)
(Demonstration by Jay Warendorff.)
“Suppose a contradiction were to be found in the axioms of set theory. Do you seriously believe that that bridge would fall down?” — Frank Ramsey, to Wittgenstein
“Does anyone believe that the difference between the Lebesgue and Riemann integrals can have physical significance, and that whether, say, an airplane would or would not fly could depend on this difference? If such were claimed, I should not care to fly in that plane.” — Richard W. Hamming
Suppose we divide a group of 100 women randomly into two groups, one of 95 and the other of 5 women. Then by flipping a fair coin we randomly assign the name “the Heads group” to one group and “the Tails group” to the other. Now philosopher John Leslie suggests that “[e]stimated probabilities can be observer-relative in a somewhat disconcerting way”:
All these persons — the women in the Heads group, those in the Tails group, and the external observer — are fully aware that there are two groups, and that each woman has a ninety-five per cent chance of having entered the larger. Yet the conclusions they ought to derive differ radically. The external observer ought to conclude that the probability is fifty per cent that the Heads group is the larger of the two. Any woman actually in [either the Heads or the Tails group], however, ought to judge the odds ninety-five to five that her group, identified as ‘the group I am in’, is the larger, regardless of whether she has been informed of its name.
Even without knowing her group’s name, a woman could still appreciate that the external observer estimated its chance of being the larger one as only fifty per cent — this being what his evidence led him to estimate in the cases of both groups. The paradox is that she herself would then have to say: ‘In view of my evidence of being in one of the groups, ninety-five per cent is what I estimate.’
Whether this is really a paradox is disputed — Oxford philosopher Nick Bostrom, in his 2002 book Anthropic Bias, points out that these are different judgments: The woman is considering the probability that she finds herself in the larger group, and the external observer is considering the assignment of labels to the groups. Bostrom describes a variant “where chances are observer relative in an interesting, but not paradoxical way” (page 129).
(John Leslie, “Observer-Relative Chances and the Doomsday Argument,” Inquiry 40:4 [1997], 427-436.)
{13, 40, 45}
The square of the sum of any two of these numbers minus the square of the third is a square:
(13 + 40)2 – 452 = 282
(13 + 45)2 – 402 = 422
(40 + 45)2 – 132 = 842
(From Edward Barbeau’s Power Play, 1997.)
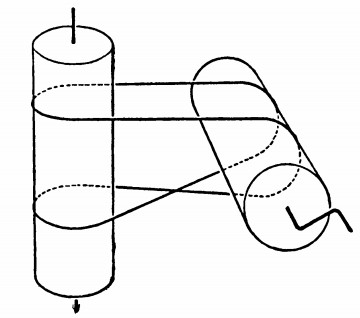
A curious phenomenon noted in Martyn Cundy and A.P. Rollett’s Mathematical Models (1951):
Two rollers are mounted on perpendicular axles in different planes. An endless thread passes round them and connects them, both directly and with a crossover, as shown in the diagram. The instrument is somewhat capricious, but the following phenomena can be demonstrated with it.
(a) One roller is rotated continuously in one direction. The other starts in one direction, but if temporarily stopped with the finger continues in the opposite direction.
(b) One roller is rotated to and fro through a small angle. The other roller rotates continuously in the same direction.
“The apparatus shows that dynamical friction is less than statical, but a full explanation is complicated, if indeed it is possible, and certainly involves consideration of the elasticity of the connecting belt.”