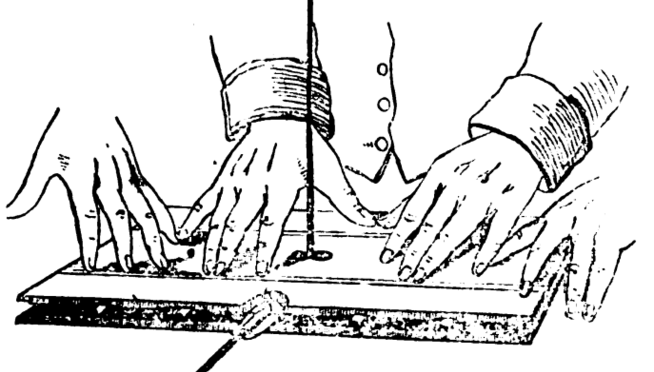
In the 1850s, when a plague of spirits began to rotate tables at London séances, Michael Faraday devised a clever way to investigate: Two boards were lain one atop the other, with an upright haystalk inserted through the pair. The experimenters laid their hands on this. The apparatus gave a way to see “whether the table moved the hand, or the hand moved the table”: If the medium willed the table to move to the left, and it did so on its own, the haystalk would be seen to lean in one direction … but if the experimenters, even unconsciously, themselves pressed the table to turn, it would lean in the other.
Faraday wrote, “As soon as the index is placed before the most earnest, and they perceive — as in my presence they have always done — that it tells truly whether they are pressing downwards only or obliquely, then all effects of table-turning cease, even though the parties persevere, earnestly desiring motion, till they become weary and worn out. No prompting or checking of the hands is needed — the power is gone; and this only because the parties are made conscious of what they are really doing mechanically, and so are unable unwittingly to deceive themselves.”
(Michael Faraday, “On Table-Turning,” Times, June 30, 1853.)




