Suppress each of the digits in 1729404 and add the resulting numbers, and you get 1729404 again:
729404 129404 179404 172404 172904 172944 + 172940 1729404
Another example:
3758846 1758846 1358846 1378846 1375846 1375846 1375886 + 1375884 13758846
Suppress each of the digits in 1729404 and add the resulting numbers, and you get 1729404 again:
729404 129404 179404 172404 172904 172944 + 172940 1729404
Another example:
3758846 1758846 1358846 1378846 1375846 1375846 1375886 + 1375884 13758846
33 = 88661289752875283 + (-8778405442862239)3 + (-2736111468807040)3
That result was discovered by Andrew Booker of the University of Bristol just this year.
It leaves 42 as the only positive integer less than 100 that has not been represented as the sum of three cubes.
(We can omit numbers that give a remainder of 4 or 5 when divided by 9, since those are known to be ineligible. But can every other integer be expressed in this way? It’s an open problem.)
(Thanks, Kate.)
09/06/2019 UPDATE: The case of 42 has now been solved, by Andrew Booker at Bristol and Andrew Sutherland at MIT:
42 = (-80538738812075974)3 + 804357581458175153 + 126021232973356313
The lowest unsolved case is now 114.
Sheep can be trained to recognize human faces, even from photographs. In a 2017 study at Cambridge University, researchers trained sheep to recognize photographs of four celebrities (Fiona Bruce, Jake Gyllenhaal, Barack Obama, and Emma Watson). They learned to distinguish a celebrity’s face from another face 8 out of 10 times, and their performance dropped only about 15% when they were shown photographs taken at an angle. When an unfamiliar photograph of a handler was inserted randomly in place of a celebrity, they chose that photo 7 out of 10 times.
“During this final task the researchers observed an interesting behaviour. Upon seeing a photographic image of the handler for the first time — in other words, the sheep had never seen an image of this person before — the sheep did a ‘double take’. The sheep checked first the (unfamiliar) face, then the handler’s image, and then unfamiliar face again before making a decision to choose the familiar face, of the handler.”
Sheep are long-lived and have relatively large brains, so it’s hoped that studying them will shed light on illnesses such as Huntington’s disease.
Also: Pigeons can distinguish Monet from Picasso, and rats can distinguish spoken Japanese from spoken Dutch. “A previous study by Porter and Neuringer (1984), who reported discrimination by pigeons between music and Bach and Stravinsky, and the present study suggest that pigeons have abilities that enable them to identify both musical and visual artists.”
Many people know that you can form a pentagon by tying a strip of paper in a simple overhand knot.
Stephen Bleecker Luce’s seamanship manual of 1863 tells how to fold a blade of grass into an octagon (below):
It is first doubled short over itself, then 1 under 2, — leaving a space, then 2 over 1, and down through the centre of the triangle; next 1 over 2, and down through the centre, coming out on the opposite side, and so on until an octagonal figure is formed.
That’s pretty terse, but I think I’ve almost managed to do it tonight. Keep your eye on the drawing of the finished piece, and don’t form and flatten the finished shape until you’ve done all the weaving.
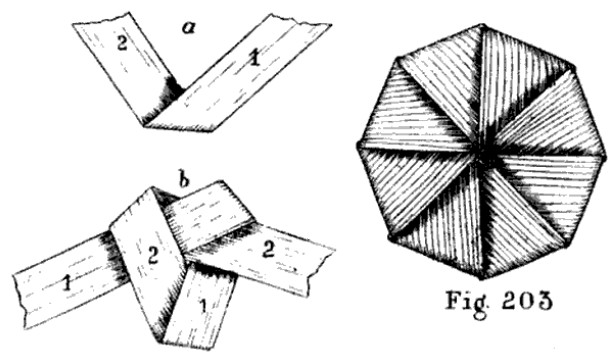
(Via The Ashley Book of Knots.)
The sum or difference of any pair of the numbers {150568, 420968, 434657} is a square:
420968 + 150568 = 7562
420968 – 150568 = 5202
434657 + 420968 = 9252
434657 – 420968 = 1172
434657 + 150568 = 7652
434657 – 150568 = 5332
Jones tells a mountain to hop into the sea and it does so. Has he performed a miracle?
Well, no, writes University of Birmingham philosopher George Chryssides. If Jones repeats his feat, then he’s revealed an underlying causal principle that’s amenable to study just like the rest of the natural world. If he doesn’t repeat the feat, then there’s no support for the idea of a link between his command and the mountain’s movement — we know only that the two events coincided, not that one caused the other.
“In order … to determine the answer to the question, ‘Did Jones move the mountain?’ … we must ascertain whether similar effects would follow similar putative causes,” Chryssides writes. “Either an allegedly miraculous event is a violation of scientific law, in which case it could not be performed by an agent, or else it is performed by an agent, in which case it could not be a violation of scientific law.”
(George D. Chryssides, “Miracles and Agents,” Religious Studies 11:3 [September 1975], 319-327.)
In the summer of 1997 mathematician Lionel Levine discovered a sequence of numbers: 1, 2, 2, 3, 4, 7, 14, 42, 213, 2837, … . It’s made up of the final term in each row of this array:
1 1
1 2
1 1 2
1 1 2 3
1 1 1 2 2 3 4
1 1 1 1 2 2 2 3 3 4 4 5 6 7
1 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 4 4 4 4 5 5 5 5 6 6 6 7 7 7 8 8 9 9 10 10 11 12 13 14
…
The array is built from a simple rule. Start with 1 1 and regard each line as a recipe for building the next one: Read it from right to left and think of it as an inventory of digits. The first line, 1 1, would be read “one 1 and one 2,” so that gives us 1 2 for the second line. The second line (again, reading from right to left) would be read “two 1s and one 2,” giving 1 1 2 for the third line.
And so on. That’s it. It’s excruciatingly simple, “yet it seems likely that the 20th term say is impossible to compute,” wrote N.J.A. Sloane that November. At that time only 15 terms were known, the last being 508009471379488821444261986503540. Two further terms have since been found, bringing us up to 5347426383812697233786139576220450142250373277499130252554080838158299886992660750432. And the 20th is still out of sight.
See the link below (page 15) for more.
(Neil J.A. Sloane, “My Favorite Integer Sequences,” in C. Ding, T. Helleseth, and H. Niederreiter, Sequences and Their Applications: Proceedings of SETA ’98, 2012, 103-130.)
In 2004, Canadian musician Andrew Huang wrote a song that encodes the first 101 digits of π.
Also: A “piku” is a haiku whose word lengths reflect the digits of π:
How I love a verse
Contrived to unhusk dryly
One image nutshell
In natural language, the most frequent word occurs about twice as often as the second most frequent word, three times as often as the third most frequent word, and so on.
In the Brown Corpus, a text collection of a million words, the most frequent word, the, accounts for 7.5% of all word occurrences, and the second most frequent, of, accounts for 3.5%. A mere 135 vocabulary items account for half the corpus, and about half the total vocabulary of about 50,000 words are hapax legomena, words that occur once only.
Similar distributions are found in data throughout the physical and social sciences; the law is named after the American linguist George Kingsley Zipf.
A set of points has diameter 1 if no two points in the set are more than 1 unit apart. An example is an equilateral triangle whose side has length 1. What’s the smallest shape that can cover any such set? A circle of diameter 1 won’t cover our triangle; part of the triangle projects beyond the circle:
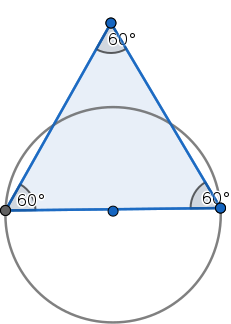
Of course a larger circle would work, but what’s the smallest shape will always do the job? Surprisingly, no one knows. When French mathematician Henri Lebesgue posed the problem to Gyula Pál in 1914, Pál suggested a modified hexagon (in black):
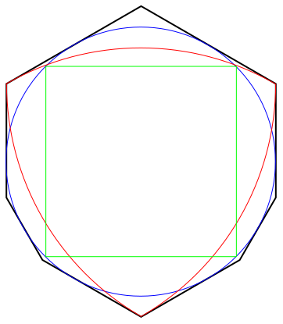
Here Pál’s shape manages to surround a circle (blue), a Reuleaux triangle (red), and a square (green), each of diameter 1, and in fact it will accommodate any such set. Its own area is 0.84529946. Will a smaller shape do the job? Well, yes, but the gains get increasingly fine: In 1936 Roland Sprague whittled Pál’s shape down to 0.844137708436, and in 1992 H.C. Hansen reduced it further to 0.844137708398. At this point observers Victor Klee and Stanley Wagon wrote, “[I]t does seem safe to guess that progress on [this problem], which has been painfully slow in the past, may be even more painfully slow in the future.” But in 2015 John Baez reached 0.8441153 with an exquisite adjustment to two regions in Hansen’s shape; the smaller of these would span only a few atoms if the shape were drawn on paper.
Is that the end of the story? No: Last October Philip Gibbs claimed a further reduction to 0.8440935944, and the search goes on. In 2005 Peter Brass and Mehrbod Sharifi showed that the universal cover must have an area of at least 0.832, so there’s room, at least in theory, for still further improvements.
(Thanks, Jacob.)