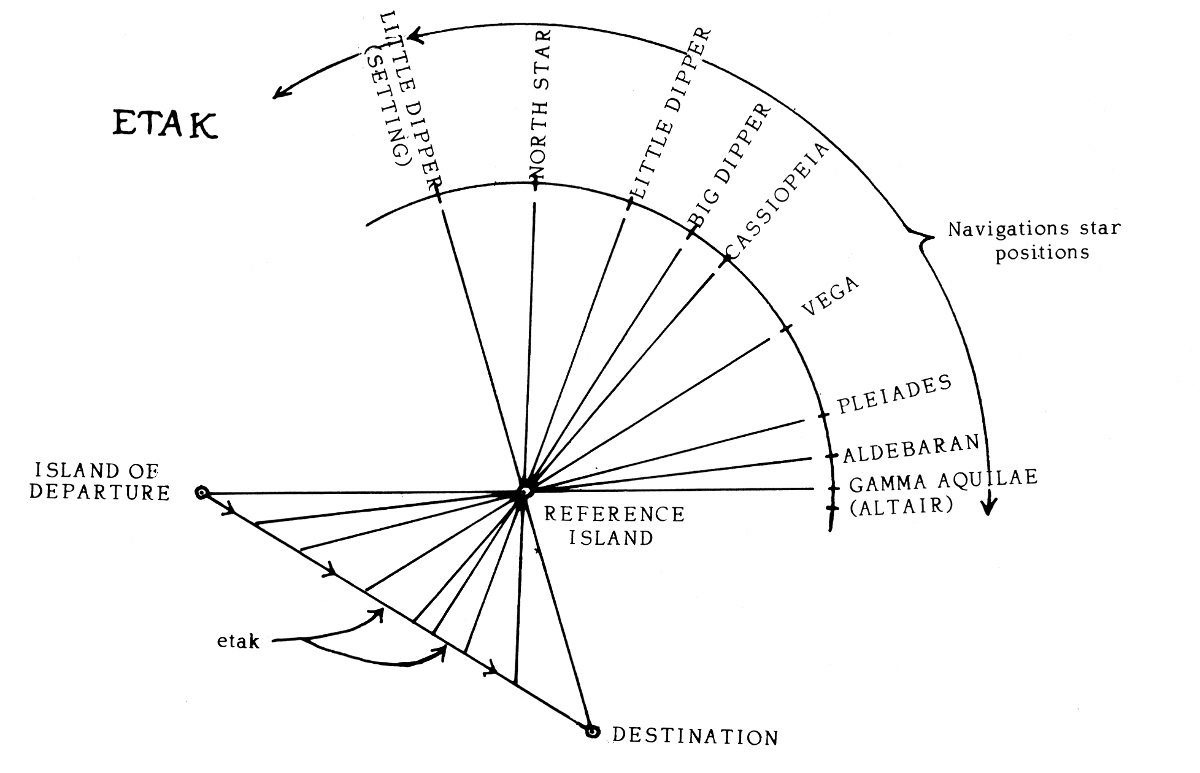
“It is true that you may fool all the people some of the time; you can even fool some of the people all the time; but you can’t fool all of the people all the time.”
This is commonly attributed to Abraham Lincoln, though it’s not clear that he actually said it. In 2004 mathematician Paul Stockmeyer noticed that its meaning is somewhat ambiguous, too. If we use P(x) to denote the predicate “x is a person,” T(y) to denote the predicate “y is a time,” and F(x, y) to denote the two-argument predicate “x is fooled at time y,” then the first phrase of the quotation, “It is true that you may fool all the people some of the time,” might mean either
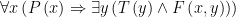
or
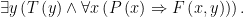
The first statement means “For every possible x, if x is a person then there exists a y such that y is a time and moreover x is fooled at time y” (or, more coloquially, “For every person, there is a time when that person is fooled”).
The second means “There exists a y such that y is a time and moreover for every x, if x is a person then x is fooled at time y (or “There is a time when everyone is simultaneously fooled”).
Which is the right interpretation? Stockmeyer polled his classes and found them nearly equally divided. And that’s only the first phrase of the quotation! Does the second phrase, “you can even fool some of the people all the time,” mean that there are people who remain constantly fooled about everything — or that you can always find a fool at any given time?
“However they are interpreted, they serve as a wonderfully effective preparation for his main point contained in the third phrase,” Stockmeyer writes. “And this phrase, with two quantifiers of the same type, is completely unambiguous.”
(Paul K. Stockmeyer, “What Did Lincoln Really Mean?” College Mathematics Journal 35:2 [2004], 103-104.)