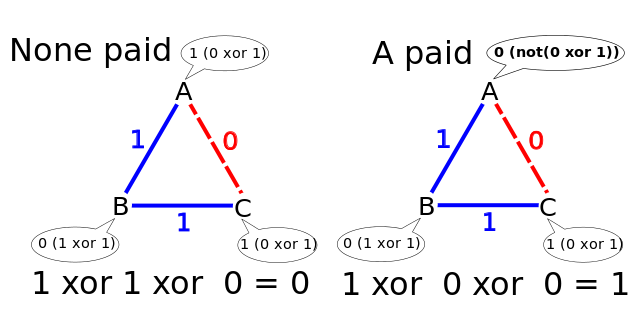
Three cryptographers are having dinner at their favorite restaurant. The waiter informs them that arrangements have been made for their bill to be paid anonymously. It may be that the National Security Agency has picked up the tab, or it may be that one of the cryptographers himself has done so. The cryptographers respect each other’s right to pay the bill anonymously, but they want to know whether the NSA is paying. Happily, there is a way to determine this without forcing a generous cryptographer to reveal himself.

Each cryptographer flips a fair coin behind a menu between himself and his right-hand neighbor, so that only the two of them can see the outcome. Then each cryptographer announces aloud whether the two coins he can see — one to his right and one to his left — had the same outcome or different outcomes. If one of the cryptographers is the payer, he states the opposite of what he sees. If an even number of cryptographers say that they saw different outcomes, then the NSA paid; if an odd number say so, then one of the cryptographers paid the bill, but his anonymity is protected.

Computer scientist David Chaum offered this example in 1988 as the basis for an anonymous communication network; these networks are often referred to as DC-nets (for “dining cryptographers”).

(David Chaum, “The Dining Cryptographers Problem: Unconditional Sender and Recipient Untraceability,” Journal of Cryptology 1:1 [1988], 65-75.)