
“There is nothing at McDonald’s that makes it necessary to have teeth.” — Harvard nutritionist Jean Mayer, Time, 1973

“There is nothing at McDonald’s that makes it necessary to have teeth.” — Harvard nutritionist Jean Mayer, Time, 1973
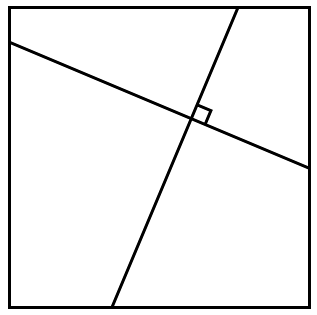
Any two lines drawn between opposite sides of a square and intersecting at right angles are equal.

In 1940 Bertrand Russell was invited to teach logic at the City College of New York.
A Mrs. Kay of Brooklyn opposed the appointment, citing Russell’s agnosticism and his alleged practice of sexual immorality.
In the lawsuit his works were described as “lecherous, libidinous, lustful, venerous, erotomaniac, aphrodisiac, irreverent, narrowminded, untruthful, and bereft of moral fiber.”
“Although he lost the case, the aging Russell was delighted to have been described as ‘aphrodisiac,'” writes Betsy Devine in Absolute Zero Gravity. “‘I cannot think of any predecessors,’ he claimed, ‘except Apuleius and Othello.'”
The quicksort computer sorting algorithm demonstrated with Hungarian folk dance, from Romania’s Sapientia University.
Also:
The four queens puzzle solved using ballet.
Binary search through flamenco dance.
Merge sort via Transylvanian-Saxon folk dance.
Selection sort using Gypsy folk dance.
(Via MetaFilter.)
01/19/2019 UPDATE: When Gavin Taylor showed these algorithms to his students at the United States Naval Academy, they asked whether they themselves could dance for extra credit. He said yes. So here are the U.S. Naval Academy midshipmen dancing the InsertionSort algorithm:
(Thanks, Gavin.)
Richard Feynman was so struck by this fact that he remembered ever afterward where he had learned it — from his childhood friend Morrie Jacobs as the two stood in Morrie’s father’s leather shop in Far Rockaway, Queens.
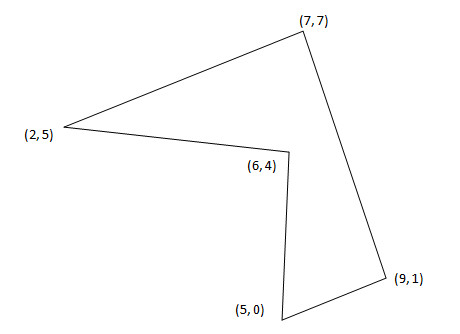
If you know the vertices of a polygon, here’s an interesting way to find its area:
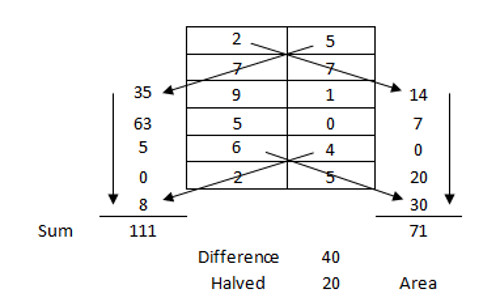
This works for any polygon, no matter the number of points, so long as it doesn’t intersect itself. It’s a slight restatement of the shoelace formula.
(Thanks, Derek, Dan, and Kyle.)
In American usage, 84,672 is said EIGHTY FOUR THOUSAND SIX HUNDRED SEVENTY TWO. Count the letters in each of those words, multiply the counts, and you get 6 × 4 × 8 × 3 × 7 × 7 × 3 = 84,672.
Brandeis University mathematician Michael Kleber calls such a number fortuitous. The next few are 1,852,200, 829,785,600, 20,910,597,120, and 92,215,733,299,200.
If you normally say “and” after “hundred” when speaking number names, then the first few fortuitous numbers are 333,396,000 (THREE HUNDRED AND THIRTY THREE MILLION, THREE HUNDRED AND NINETY SIX THOUSAND), 23,337,720,000, 19,516,557,312,000, 56,458,612,224,000, and 98,802,571,392,000.
And 54 works in both French and Russian.
(Michael Kleber, “Four, Twenty-Four, … ?,” Mathematical Intelligencer 24:2 [March 2002], 13-14.)
A.F. Bainbridge of British Aerospace noticed this curiosity in 1991. On a calculator keypad like this:
1 2 3 4 5 6 7 8 9
… choose two three-digit numbers (say, 435 and 667) and multiply them (290145). Now use symmetrical paths on the keyboard to find two “complementary” numbers (that is, symmetrical across the center, here 675 and 443) and multiply those (299025).
The difference between these two products (299025 – 290145 = 8880) will always be evenly divisible by 37.
(A.F. Bainbridge and P.A. Binding, “Symmetrical Paths on a Calculator,” Mathematical Gazette 75:474 [December 1991], 399-401.)
https://www.youtube.com/watch?v=UDBAT-gW6hg
Kohta Suzuno of Japan’s Meiji University has devised a way to solve mazes using the Marangoni effect: Fill the maze with milk, place an acidic hydrogel block at the exit, and introduce dye and a soap at the entrance. The pH change alters the surface tension and drives the dye toward the block. “In a typical experiment, the shortest path can be found and visualized within ~10s.” Suzuno has even used this technique to find the shortest distance between two points in Budapest, using a maze modeled on a street map.
(Kohta Suzuno et al., “Marangoni Flow Driven Maze Solving,” in A. Adamatzky, ed., Advances in Unconventional Computing, Vol. 23, 2017.)
Andrew Bremner devised a magic square that expresses 652 as the sum of three squares in six different ways (the sum of each row and column):
152 202 602
362 482 252
522 392 02
(From Edward Barbeau, Power Play, 1997.)