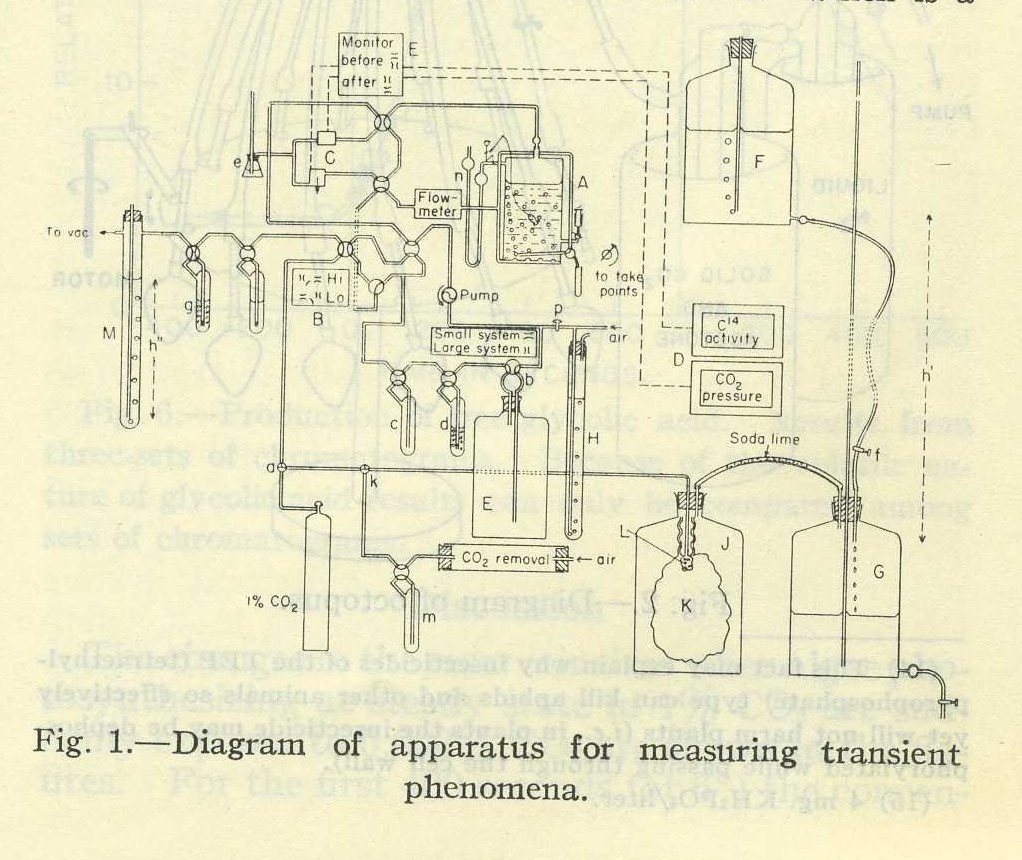
From the Royal Society of Chemistry’s Chemistry World blog: In 1955, when impish graduate student A.T. Wilson published a paper with his humorless but brilliant supervisor, Melvin Calvin, Wilson made a wager with a department secretary that he could sneak a picture of a man fishing into one of the paper’s diagrams. He won the wager — can you find the fisherman?
Science & Math
“Algebraic Theory of French Letters”
From Lee Sallows:
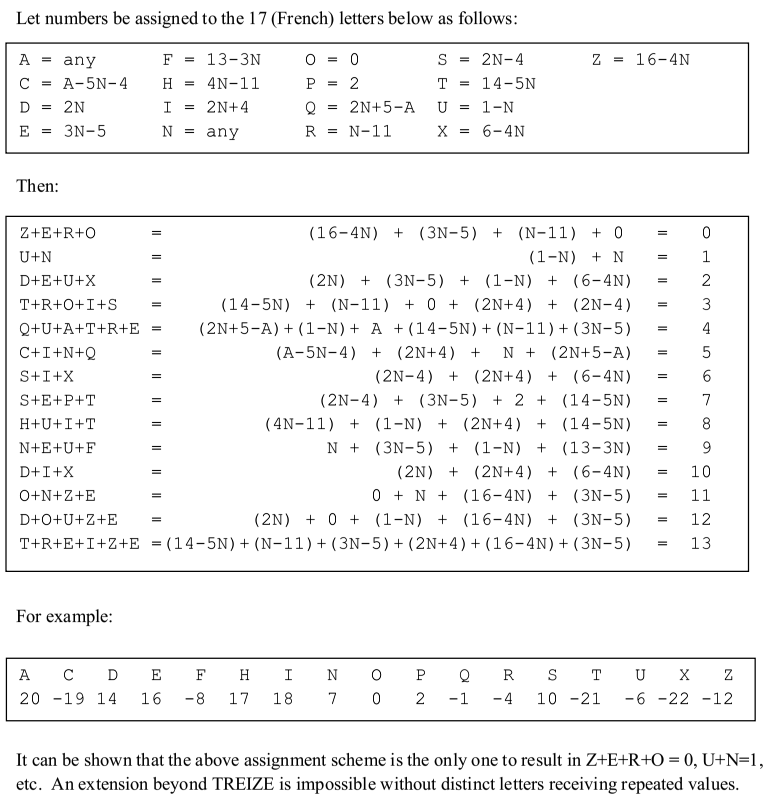
(Thanks, Lee!)
Plutchik’s Wheel of Emotions
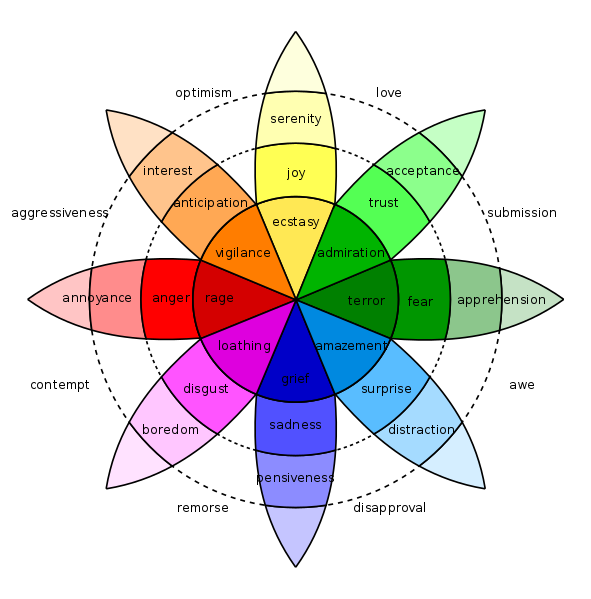
In 1958 psychologist Robert Plutchik suggested that there are eight primary emotions: joy, sadness, anger, fear, trust, disgust, surprise, and anticipation. Each of the eight exists because it serves an adaptive role that gives it survival value — for example, fear inspires the fight-or-flight response.
He arranged them on a wheel to show their relationships, with similar emotions close together and opposites 180 degrees apart. Like colors, emotions can vary in intensity (joy might vary from serenity to ecstasy), and they can mix to form secondary emotions (submission is fear combined with trust, and awe is fear combined with surprise).
When all these combinations are included, the system catalogs 56 emotions at 1 intensity level. And in his final “structural model” of emotions, the petals are folded up in a third dimension to form a cone.
Dictum

Hunters of the 19th century defended their practice in part because it was the only way to identify species that would otherwise remain unknown.
They distilled this into an adage: “What’s hit is history, what’s missed is mystery.”
Art Appreciation

In 1833, to show that vultures found their prey by sight rather than smell, naturalist John Bachman made “a coarse painting representing a sheep skinned and cut open”:
This proved very amusing — no sooner was this picture placed on the ground than the Vultures observed it, alighted near, walked over it, and some of them commenced tugging at the painting. They seemed much disappointed and surprised, and after having satisfied their curiosity, flew away. This experiment was repeated more than fifty times, with the same result.
He confirmed the result by setting the painting within two feet of a heap of camouflaged offal in his garden. “They came as usual, walked around it, but in no instance evinced the slightest symptoms of their having scented the offal which was so near them.” He concluded that, while vultures may have a sense of smell, they don’t use it to find food.
See Vulture Picnic.
Memory Limit
In 1956 Harvard psychologist George Miller pointed out a pattern he’d observed. If a person is trained to respond to a given pitch with a corresponding response, she’ll respond nearly perfectly when up to six pitches are involved, but beyond that her performance declines. Humans seem to have an “information channel capacity” of 2-3 bits of information: We can distinguish among 4-8 alternatives and respond appropriately, but beyond that number we start to founder.
A similar limit appears in studies of memory span. One psychologist read aloud lists of random items at a rate of one per second and then asked subjects to repeat what they’d heard. No matter what items had been read — words, letters, or numbers — people could store a maximum of about seven unrelated items at a time in their immediate memory.
It’s probably only a coincidence that these tasks have similar limits, but it’s still a useful rule of thumb: The number of objects an average person can hold in working memory is about seven.
(George A. Miller, “The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information,” Psychological Review 63:2 [1956], 81-97.)
Pi Clacks
In 2003 mathematician Gregory Galperin of Eastern Illinois University offered a remarkable way to calculate π: Launch two masses toward an elastic wall, count the resulting collisions, and you can generate π to any precision, at least in principle.
“On the one hand, our method is purely mathematical and, most likely, will never be used as a practical way for finding approximations of π. On the other hand, this method is the simplest one among all the known methods (beginning from the ancient Greeks!).”
The video above, by 3Blue1Brown, gives the setup; the continuation is below. Via MetaFilter.
(Gregory Galperin, “Playing Pool With π (The Number π From a Billiard Point of View),” Regular and Chaotic Dynamics 8:4 [2003], 375-394.)
Strange Encounter

In June 1867 French astronomer Camille Flammarion was floating west from Paris in a balloon when he entered a region of dense cloud:
Suddenly, whilst we are thus suspended in the misty air, we hear an admirable concert of instrumental music, which seems to come from the cloud itself and from a distance of a few yards only from us. Our eyes endeavour to penetrate the depths of white, homogeneous, nebulous matter which surrounds us in every direction. We listen with no little astonishment to the sounds of the mysterious orchestra.
The cloud’s high humidity had concentrated the sound of a band playing in a town square more than a kilometer below. Five years earlier, during his first ascent over Wolverhampton in July 1862, James Glaisher had heard “a band of music” playing at an elevation of nearly 4 kilometers (13,000 feet).
(From Glaisher’s Travels in the Air, 1871.)
Podcast Episode 235: Leon Festinger and the Alien Apocalypse

In 1955, aliens from the planet Clarion contacted a Chicago housewife to warn her that the end of the world was imminent. Psychologist Leon Festinger saw this as a unique opportunity to test a new theory about human cognition. In this week’s episode of the Futility Closet podcast we’ll follow him inside a UFO religion as it approaches the apocalypse.
We’ll also try to determine when exactly LBJ became president and puzzle over some wet streets.
Rubik’s Clock

Hungarian sculptor and architect Ernő Rubik presented this puzzle in 1988; it was originally created by Christopher C. Wiggs and Christopher J. Taylor. The puzzle has two sides, with nine clocks on each side, and the goal is to set all the clocks to 12 o’clock simultaneously.
There are two ways to adjust the clocks. Turning a wheel at any of the four corners will adjust the clock at that corner on both sides of the puzzle. And turning a wheel will also adjust the three clocks adjacent to that corner on one side of the puzzle or the other; which side is determined by the four buttons surrounding the central clock.
So, for example, pressing the northwest button “in” and then turning the northwest wheel will adjust the northwestern quartet of clocks and the corresponding corner clock on the other side of the puzzle. Pulling the northwest button “out” and turning the same wheel will adjust the northwestern clock on the front of the puzzle, its counterpart on the back, and the three clocks adjacent to it on that side.
This is more intuitive than it sounds. Here’s a simulator.
Since there are 14 independent clocks, with 12 settings each, there are a total of 1214 = 1,283,918,464,548,864 possible configurations. It turns out that no configuration requires more than 12 moves to solve; for comparison, in the “worst case” solving a Rubik’s cube can take 20 moves. The trouble, of course, is knowing how to go about it.