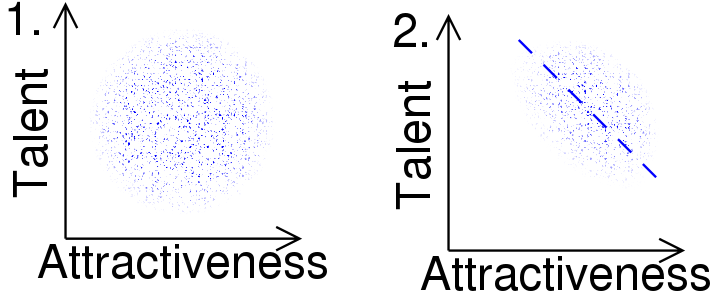
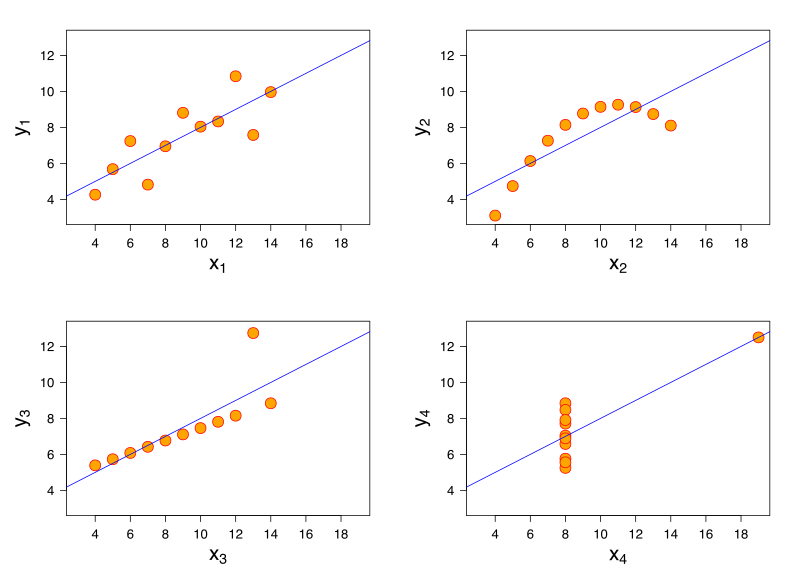
The young specialist in English Lit … lectured me severely on the fact that in every century people have thought they understood the Universe at last, and in every century they were proved to be wrong. It follows that the one thing we can say about our modern ‘knowledge’ is that it is wrong.
… My answer to him was, ‘… when people thought the Earth was flat, they were wrong. When people thought the Earth was spherical they were wrong. But if you think that thinking the Earth is spherical is just as wrong as thinking the Earth is flat, then your view is wronger than both of them put together.’
— Isaac Asimov, The Relativity of Wrong, 1989
(J.R. Deller Jr. wrote, “Education is the process of telling smaller and smaller lies.”)