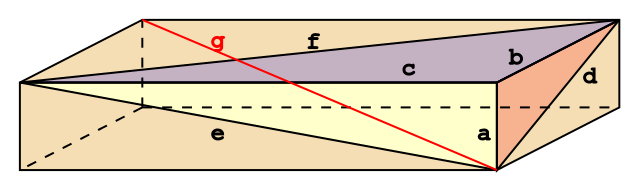
Certainly rectangular cuboids exist whose edges and face diagonals all have integer lengths.

For example, in 1719 Paul Halcke discovered one with edges (a, b, c) = (44, 117, 240) and face diagonals (d, e, f ) = (125, 244, 267).

But does one exist whose space diagonal (here shown in red) also has integer length?

As of last September, none has been found and no one has proven that none exist.