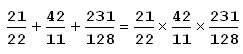
Science & Math
Ranks and Files
From Ross Honsberger via Martin Gardner: Deal cards into any rectangular array:

Put each row into numerical order:

Now put each column into numerical order:

Surprisingly, that last step hasn’t disturbed the preceding one — the rows are still in order. Why?
Future Perfect

While browsing around the library one day, I notice an old dusty tome, quite large, entitled ‘Alvin I. Goldman.’ I take it from the shelf and start reading. In great detail, it describes my life as a little boy. It always gibes with my memory and sometimes even revives my memory of forgotten events. I realize that this purports to be a book of my life and I resolve to test it. Turning to the section with today’s date on it, I find the following entry for 2:36 p.m. ‘He discovers me on the shelf. He takes me down and starts reading me …’ I look at the clock and see that it is 3:03. It is quite plausible, I say to myself, that I found the book half an hour ago. I turn now to the entry for 3:03. It reads: ‘He is reading me. He is reading me. He is reading me.’ I continue looking at the book in this place, meanwhile thinking how remarkable the book is. The entry reads: ‘He continues to look at me, meanwhile thinking how remarkable I am.’
I decide to defeat the book by looking at a future entry. I turn to an entry 18 minutes hence. It says: ‘He is reading this sentence.’ Aha, I say to myself, all I need do is refrain from reading that sentence 18 minutes from now. I check the clock. To ensure that I won’t read that sentence, I close the book. My mind wanders; the book has revived a buried memory and I reminisce about it. I decide to reread the book and relive the experience. That’s safe, I tell myself, because it is an earlier part of the book. I read that passage and become lost in reverie and rekindled emotion. Time passes. Suddenly I start. Oh yes, I intended to refute the book. But what was the time of the listed action?, I ask myself. It was 3:19, wasn’t it? But it’s 3:21 now, which means I have already refuted the book. Let me check and make sure. I inspect the book at the entry for 3:17. Hmm, that seems to be the wrong place, for there it says I’m in a reverie. I skip a couple pages and suddenly my eyes alight on the sentence: ‘He is reading this sentence.’ But it’s an entry for 3:21, I notice! So I made a mistake. The action I had intended to refute was to occur at 3:21, not 3:19. I look at the clock, and it is still 3:21. I have not refuted the book after all.
— Alvin I. Goldman, “Actions, Predictions, and Books of Life,” American Philosophical Quarterly, 1968
Goldman’s point is not that determism is true, but that it could be. It’s possible to imagine a determined universe, even one in which your own actions are accurately predicted, that unfolds in a way that makes it appear quite similar to our own. “The fact that this imagined world is determined and contains predictions of acts, and yet resembles the real world very closely, suggests to me that the real world may also be determined,” Goldman writes. Might it?
Even Odds
A bag contains 16 billiard balls, some white and some black. You draw two balls at the same time. It is equally likely that the two will be the same color as different colors. What is the proportion of colors within the bag?
Tempest-Tost
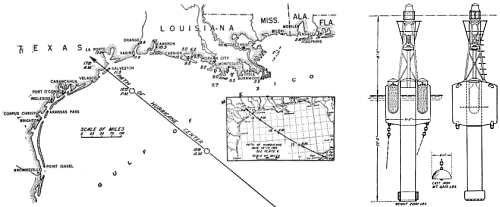
As the hurricane of August 1915 approached Galveston, Texas, it encountered a buoy in the Gulf of Mexico.
Investigators later found the buoy nearly 10 miles west of its original location.
It weighed 21,000 pounds and had been anchored with a 6,500-pound sinker and 252 feet of chain weighing 3,250 pounds.
Misc
- No point in Great Britain is more than 75 miles from the sea.
- MOONLIGHT = THIN GLOOM
- 2427 = 21 + 42 + 23 + 74
- Sweden had a Charles VII, but no Charleses I-VI.
- “If a man who cannot count finds a four-leaf clover, is he entitled to happiness?” — Stanislaw Lec
Hollis’ Paradox

You are sharing a train compartment with two strangers, A and B. You and A each think of a positive integer and whisper it to B. B stands up and says, “This is my stop. You have each thought of a different number. Neither of you can deduce which number is bigger.” He leaves.
You and A regard one another across the compartment. You think, “He cannot have chosen 1, because then he would know immediately that my number is bigger. And he can apply the same reasoning to my number. So it’s certain that neither of us has chosen 1. But once we’ve established that, then it’s equally clear that neither of us can have chosen 2, for the same reason.”
It would seem that you can extend this line of reasoning to include any number you like — including 157, the number you picked. How can this be?
See The Necktie Paradox and Tug of War.
Creative Solutions
Faced with the simultaneous equations
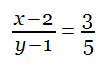
and
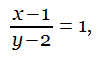
a lazy student ignored the second equation and solved the first in this way:
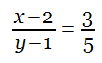
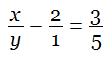
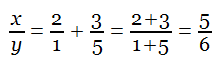
and hence x = 5 and y = 6. As it happens, that’s correct. Maurice Kraitchik writes, “Can you blame him for his answer?”
In Mathematical Circles Revisited, Howard Eves tells of “Hapless Harry,” who tackled
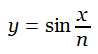
by writing
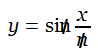
and
![]()
Math Notes
1/998001 = 0.000001002003004005006007008009010011012013014015016017018019020 0210220230240250260270280290300310320330340350360370380390400410420430440450 4604704804905005105205305405505605705805906006106206306406506606706806907007 1072073074075076077078079080081082083084085086087088089090091092093094095096 0970980991001011021031041051061071081091101111121131141151161171181191201211 2212312412512612712812913013113213313413513613713813914014114214314414514614 7148149150151152153154155156157158159160161162163164165166167168169170171172 1731741751761771781791801811821831841851861871881891901911921931941951961971 9819920020120220320420520620720820921021121221321421521621721821922022122222 3224225226227228229230231232233234235236237238239240241242243244245246247248 2492502512522532542552562572582592602612622632642652662672682692702712722732 7427527627727827928028128228328428528628728828929029129229329429529629729829 9300301302303304305306307308309310311312313314315316317318319320321322323324 3253263273283293303313323333343353363373383393403413423433443453463473483493 5035135235335435535635735835936036136236336436536636736836937037137237337437 5376377378379380381382383384385386387388389390391392393394395396397398399400 4014024034044054064074084094104114124134144154164174184194204214224234244254 2642742842943043143243343443543643743843944044144244344444544644744844945045 1452453454455456457458459460461462463464465466467468469470471472473474475476 4774784794804814824834844854864874884894904914924934944954964974984995005015 0250350450550650750850951051151251351451551651751851952052152252352452552652 7528529530531532533534535536537538539540541542543544545546547548549550551552 5535545555565575585595605615625635645655665675685695705715725735745755765775 7857958058158258358458558658758858959059159259359459559659759859960060160260 3604605606607608609610611612613614615616617618619620621622623624625626627628 6296306316326336346356366376386396406416426436446456466476486496506516526536 5465565665765865966066166266366466566666766866967067167267367467567667767867 9680681682683684685686687688689690691692693694695696697698699700701702703704 7057067077087097107117127137147157167177187197207217227237247257267277287297 3073173273373473573673773873974074174274374474574674774874975075175275375475 5756757758759760761762763764765766767768769770771772773774775776777778779780 7817827837847857867877887897907917927937947957967977987998008018028038048058 0680780880981081181281381481581681781881982082182282382482582682782882983083 1832833834835836837838839840841842843844845846847848849850851852853854855856 8578588598608618628638648658668678688698708718728738748758768778788798808818 8288388488588688788888989089189289389489589689789889990090190290390490590690 7908909910911912913914915916917918919920921922923924925926927928929930931932 9339349359369379389399409419429439449459469479489499509519529539549559569579 5895996096196296396496596696796896997097197297397497597697797897998098198298 3984985986987988989990991992993994995996997999 ...
(Thanks, William.)
The Tempest Prognosticator

Naturalist George Merryweather offered a gruesome new instrument at London’s Great Exhibition in 1851: He imprisoned 12 leeches in a ring of bottles, which he capped with whalebone levers. (The bottles were arranged in a circle so that the leeches “might see one another and not endure the affliction of solitary confinement.”) When a storm approached, the agitated leeches would climb the bottles, trip the levers, and ring a bell. The more agitated this “jury of philosophical councilors,” the more frequently the bell sounded, and the more likely a storm.
After a year of experiments, Merryweather claimed great success — among other feats, the “leech barometer” foretold the disastrous storm of October 1850 51 hours before it took place. “I may here observe,” Merryweather wrote, “that I could cause a little leech, governed by its instinct, to ring Saint Paul’s great bell in London as a signal for an approaching storm.”
He proposed that the government install stations around the British coast, and nominated engineer William Reid to be inspector-general of leeches and meteorologist James Glaisher his second-in-command. Inexplicably, they turned him down. “After this,” opined Chambers’ Journal, “the Snail Telegraph looks not quite so outrageous an absurdity.”
