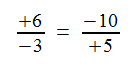In logic, the contrapositive of “If A, then B” is “If not B, then not A”: “If Socrates is a man, then Socrates is human” carries the same message as “If Socrates is not human, then Socrates is not a man.”
To make this vivid for his geometry students, W.P. Cooke of West Texas State University enlisted Tex Ritter’s song “Rye Whiskey”:
If the ocean was whiskey and I was a duck,
I’d swim to the bottom and never come up.
But the ocean ain’t whiskey and I ain’t no duck,
So I’ll play Jack-O-Diamonds and trust to my luck.
For it’s whiskey, rye whiskey, rye whiskey, I cry,
If I don’t get rye whiskey, I surely will die.
In contrapositive form, Cooke said, Ritter would sing:
If I never reach bottom or sometimes come up,
Then the ocean ain’t whiskey or I ain’t a duck.
But my luck can’t be trusted or the cards I’ll not buck,
So the ocean is whiskey or I am a duck.
For it’s whiskey, rye whiskey, rye whiskey, I cry,
If my death is uncertain then I get whiskey (rye).
(American Mathematical Monthly, November 1969)
01/31/2012 Related:
Andrew Marvell’s “To His Coy Mistress” is constructed as a three-paragraph logical argument:
“Had we but world enough, and time,
This coyness, lady, were no crime…”
(If A, then B)
“But at my back I always hear
Time’s winged chariot hurrying near…”
(Not A)
“Now therefore, while the youthful hue
Sits on thy skin like morning dew…
Now let us sport us while we may…”
(Therefore Not B)
Unfortunately, he’s trying to argue his way from “If A, then B” to “Not A, therefore not B,” which is invalid. One wonders how his coy mistress responded.
(Thanks, Cleve.)