- Asked to invent the perfect bestselling title, Bennett Cerf suggested Lincoln’s Doctor’s Dog.
- The two most common birthdates for Nobel laureates are May 21 and February 28 (seven apiece).
- ALASKA is the only U.S. state name that can be typed on a single row of keys on a standard typewriter.
- 13177388 = 71 + 73 + 71 + 77 + 77 + 73 + 78 + 78
- “I don’t know much about medicine, but I know what I like.” — S.J. Perelman
Science & Math
Two Squares
Retired Pittsburgh math teacher Walter W. Horner devised this doubly magic square in 1955:
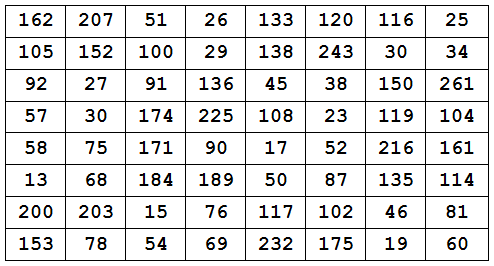
Each row, column, and long diagonal produces both a sum of 840 and a product of 2058068231856000.
And Rodolfo Marcelo Kurchan of Buenos Aires discovered this remarkable square in 1991:
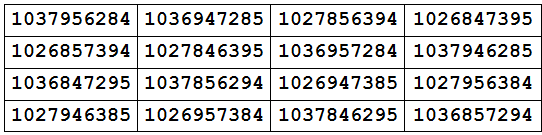
Each number contains all 10 digits — and so does the magic sum, 4129607358.
Wise Cracks
In 1998, California physician Donald L. Unger wrote to the editors of Arthritis & Rheumatism to report a “50-year controlled study by one participant.” His mother had told him that cracking his knuckles would lead to arthritis, so for 50 years the science-minded Unger had cracked the knuckles of his left hand at least twice a day, more than 36,500 times in all, and left the right uncracked as a control. After 50 years he found no arthritis in either hand and no differences between the two hands.
“This result calls into question whether other parental beliefs, e.g., the importance of eating spinach, are also flawed,” Unger wrote. “Further investigation is likely warranted.”
The editors invited a response from Robert L. Swezey, who had published an earlier investigation in the Western Journal of Medicine. Swezey said that his own study had been inspired when his 12-year-old son’s grandmother had warned him that cracking his knuckles would cause arthritis. “It is now 22 years later and he continues to enjoy frequent KC without manifestations or evidence of arthritis.”
With motherly advice thrown into doubt, Swezey wondered whether knuckle cracking might even prevent osteoarthritis. “The possible utilization of KC by managed care providers as an economic, noninvasive, home preventative treatment for arthritis of the hands should be given further consideration,” he concluded. “A clear distinction between hand wringing related to managed care procedures and therapeutic KC will have to be made.”
(Does knuckle cracking lead to arthritis of the fingers? Unger DL. Arthritis Rheum. 1998 May;41(5):949-50.) (Thanks, Bob.)
Misc
- Kurt Vonnegut managed the country’s first Saab dealership.
- Max Born is Olivia Newton-John’s grandfather.
- 19683 = 1 × (9 – 6)8 × 3
- Before the advent of European settlers, it’s believed that no Native American had blood type B.
- “Good taste is the worst vice ever invented.” — Edith Sitwell
The first recorded performance of Hamlet took place at sea, aboard the East India ship Red Dragon off the coast of Africa in 1607. Capt. William Keeling’s diary entry for Sept. 5 reads: “I sent the interpreter according to his desier abord the Hector whear he brooke fast and after came abord me wher we gave the tragedie of Hamlett.”
Time and Motion
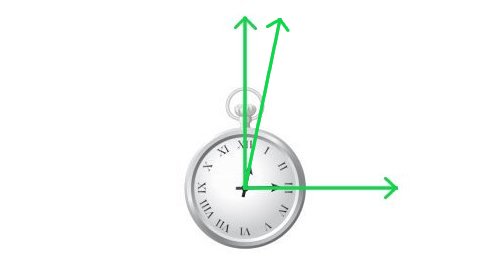
It’s impossible to trisect an angle using a compass and a straightedge, but in 1947 Leo Moser showed how to do it with a pocketwatch. At noon align the watch’s hands with one side of the angle (above, XII), then wait until the minute hand has crossed to the other side (III). At that point the hour hand will have measured one-twelfth of the angle. Double that twice and you have your trisection.
“Now you can trisect an angle anytime, anyplace, for anyone who asks,” writes Underwood Dudley in A Budget of Trisections. “But no one ever will.”
Corner Market
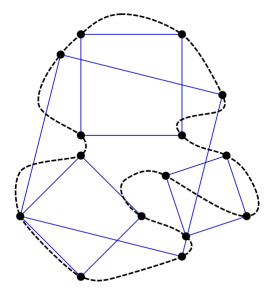
Does every closed curve contain the vertices of a square?
No one knows.
Math Notes

Misc
- James Buchanan’s niece was his first lady.
- FIVE THOUSAND is the highest number name with no repeated letters.
- Ardmore, Tennessee, borders Ardmore, Alabama.
- 9306 × 2013 = 3102 × 6039
- “So that’s what hay looks like.” — Queen Mary
If God exists outside space and time, then how can he be omnipresent, present in all places at all times? If he exists within it, how could he have created it? How could a creation (or anything) take place outside time?
Math Notes
2015 = 4 + 8 + 4 + 9 + 3 + 3 + 1 + 9 + 6 + 7 + 7 + 7 + 1 + 1 + 4 + 0 + 7 + 4 + 1 + 4 + 3 + 9 + 5 + 8 + 6 + 0 + 1 + 2 + 9 + 6 + 0 + 4 + 7 + 1 + 9 + 1 + 3 + 0 + 3 + 2 + 3 + 8 + 8 + 8 + 8 + 3 + 2 + 8 + 4 + 9 + 3 + 7 + 8 + 8 + 8 + 9 + 3 + 4 + 1 + 7 + 1 + 2 + 4 + 6 + 3 + 6 + 4 + 6 + 1 + 2 + 8 + 2 + 5 + 3 + 5 + 5 + 3 + 5 + 1 + 9 + 7 + 0 + 3 + 0 + 8 + 1 + 3 + 9 + 9 + 2 + 8 + 9 + 5 + 7 + 8 + 3 + 3 + 0 + 8 + 5 + 9 + 5 + 6 + 8 + 3 + 2 + 6 + 3 + 1 + 8 + 8 + 3 + 5 + 1 + 0 + 9 + 0 + 1 + 9 + 6 + 3 + 2 + 2 + 5 + 1 + 3 + 8 + 3 + 9 + 4 + 4 + 5 + 9 + 5 + 9 + 2 + 7 + 1 + 1 + 5 + 7 + 6 + 4 + 9 + 5 + 1 + 8 + 0 + 4 + 1 + 5 + 4 + 0 + 1 + 8 + 3 + 1 + 4 + 6 + 5 + 9 + 6 + 1 + 7 + 1 + 1 + 0 + 2 + 0 + 2 + 2 + 8 + 3 + 0 + 0 + 8 + 9 + 6 + 5 + 0 + 2 + 9 + 2 + 1 + 7 + 7 + 5 + 8 + 7 + 7 + 9 + 7 + 2 + 9 + 0 + 1 + 8 + 8 + 6 + 9 + 1 + 2 + 8 + 2 + 7 + 7 + 5 + 4 + 3 + 6 + 0 + 9 + 5 + 4 + 1 + 0 + 1 + 0 + 0 + 3 + 8 + 4 + 0 + 4 + 2 + 1 + 8 + 1 + 2 + 8 + 9 + 4 + 6 + 0 + 8 + 3 + 7 + 6 + 3 + 8 + 8 + 8 + 5 + 5 + 9 + 2 + 4 + 7 + 7 + 5 + 3 + 0 + 7 + 4 + 6 + 1 + 6 + 8 + 6 + 4 + 3 + 7 + 0 + 2 + 5 + 8 + 1 + 3 + 7 + 9 + 8 + 7 + 3 + 3 + 6 + 3 + 4 + 7 + 5 + 8 + 8 + 5 + 2 + 6 + 5 + 6 + 6 + 6 + 6 + 0 + 8 + 6 + 0 + 6 + 6 + 9 + 0 + 8 + 2 + 5 + 6 + 1 + 1 + 3 + 2 + 6 + 9 + 6 + 0 + 9 + 4 + 5 + 2 + 4 + 2 + 5 + 1 + 2 + 5 + 7 + 6 + 8 + 8 + 0 + 6 + 9 + 9 + 8 + 7 + 1 + 3 + 4 + 0 + 9 + 4 + 6 + 1 + 5 + 0 + 8 + 4 + 3 + 6 + 8 + 3 + 1 + 5 + 2 + 3 + 4 + 0 + 1 + 0 + 3 + 5 + 3 + 4 + 1 + 8 + 1 + 0 + 3 + 2 + 6 + 6 + 3 + 0 + 1 + 4 + 1 + 9 + 3 + 7 + 7 + 6 + 8 + 2 + 0 + 6 + 8 + 2 + 7 + 2 + 3 + 6 + 4 + 4 + 3 + 4 + 2 + 2 + 2 + 3 + 9 + 8 + 5 + 3 + 6 + 2 + 0 + 2 + 1 + 6 + 5 + 9 + 5 + 6 + 6 + 3 + 0 + 8 + 0 + 7 + 2 + 4 + 7 + 5 + 4 + 0 + 4 + 6 + 0 + 0 + 2 + 5 + 4 + 4 + 7 + 8 + 2 + 8 + 2 + 2 + 9 + 5 + 1 + 6 + 7 + 4 + 4 + 6 + 1 + 3 + 6 + 4 + 7 + 4 + 6 + 0 + 9 + 3 + 7 + 5
2015137 = 484933196777114074143958601296047191303238888328493788893417124636461282
535535197030813992895783308595683263188351090196322513839445959271157649518041540
183146596171102022830089650292177587797290188691282775436095410100384042181289460
837638885592477530746168643702581379873363475885265666608606690825611326960945242
512576880699871340946150843683152340103534181032663014193776820682723644342223985
362021659566308072475404600254478282295167446136474609375
(Thanks, Pablo.)
Misc
- Most Muppets are left-handed.
- The largest prime number in the Bible is 22273 (Numbers 3:43).
- SEE, HE, and IS are spelled identically in Morse code (ignoring spaces).
- Maine is the only one-syllable state name.
- “More things grow in the garden than the gardener sows.” — Spanish proverb
Fritz Zwicky referred to his colleagues at the Mount Wilson Observatory as “spherical bastards” because they were bastards whichever way one looked at them.
