Another remarkable contribution by Lee Sallows:

(Thanks, Lee!)
Another remarkable contribution by Lee Sallows:

(Thanks, Lee!)
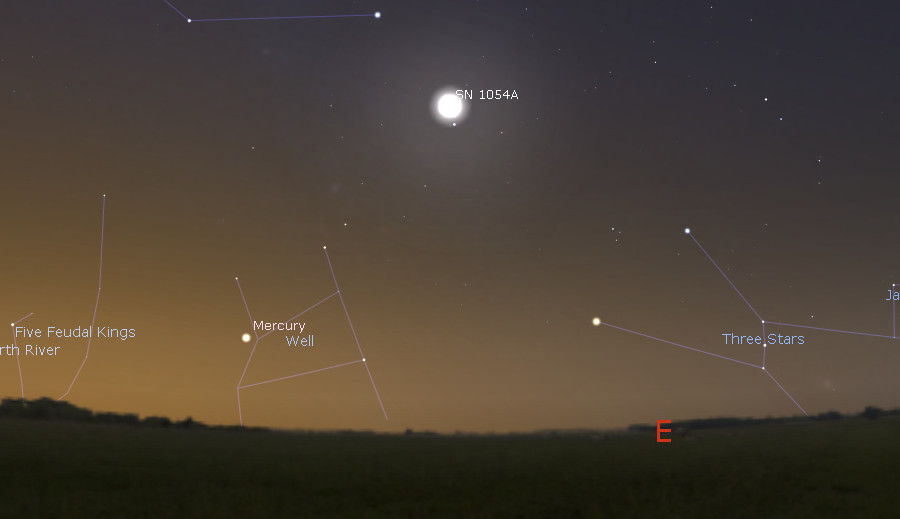
In July 1054 Chinese astronomers saw a reddish-white star appear in the eastern sky, its “rays stemming in all directions.” Yang Weide wrote:
I humbly observe that a guest star has appeared; above the star there is a feeble yellow glimmer. If one examines the divination regarding the Emperor, the interpretation is the following: The fact that the star has not overrun Bi and that its brightness must represent a person of great value. I demand that the Office of Historiography is informed of this.
It’s now believed they were witnessing SN 1054 — the supernova that gave birth to the Crab Nebula.
If Chicken McNuggets come in packs of 6, 9, and 20, what’s the largest number of McNuggets that you can’t buy?
Steve Omohundro and Peter Blicher posed this question in MIT Technology Review in May 2002, and Ken Rosato contributed a neat solution.
The answer is 43. To start, notice that we can use the 6-packs and 9-packs to piece together any multiple of 3 other than 3 itself. 43 itself is not divisible by 3, so 6-packs and 9-packs alone won’t get us there, and adding some 20-packs won’t help, since we’d have to add them to a quantity of either 23 or 3, neither of which can be assembled from packs of other sizes. So that shows that 43 itself can’t be reached.
But we still need to show that every larger number can be. Well, we can create all the larger even numbers by adding some quantity of 6-packs to either 36, 38, or 40, and each of those foundations can be assembled from the packs we have (36 = 9 + 9 + 9 + 9, 38 = 20 + 9 + 9, and 40 = 20 + 20). So that takes care of the even numbers. And adding 9 to any of these even numbers will give us any desired odd number above 43, starting with 36 + 9 = 45.
So 43 is the largest number of Chicken McNuggets that can’t be formed by combining 6-packs, 9-packs, and 20-packs.
(I think Henri Picciotto was the first to broach this arresting question, in Games magazine in 1987. Since then, McNuggets have found their way into Happy Meals in 4-piece servings, reducing the largest non–McNugget number to 11. In some countries, though, the 9-piece allotment has been increased to 10 — and in that case there is no largest such number, as no odd quantity can ever be assembled.)

In their 1981 book Facts and Fallacies, Chris Morgan and David Langford note that the biblical reference to the “four corners of the earth” would apply equally well if the world were a tetrahedron.
In a similar spirit, as American airman Joseph Portney was flying over the North Pole in 1968 he wondered, “What if the Earth were … ?” He made sketches of 12 fanciful alternate Earths and gave them to Litton’s Guidance & Control Systems graphic arts group, which created models that were featured in the company’s Pilots and Navigators Calendar of 1969. This made an international sensation, and Portney’s creations were subsequently published for use in classrooms worldwide, inviting students to ponder what life would be like on a cone or a dodecahedron.
Portney graduated from the U.S. Naval Academy and went on to work for Litton on high-altitude navigation problems — for example, designing control systems that could guide an aircraft around one of these strange worlds.
Consider the set (2, 5, 9, 13). Which of these numbers can be tossed out, and for what reason?
We might choose:
“Hence one could toss out either 2, 9 or 13,” observes Marquette University mathematician George R. Sell. “Therefore one should toss out 5 because it is the only number that cannot be tossed out.”
(George R. Sell, “A Paradox,” Pi Mu Epsilon Journal 2:6 [Spring 1957], 278.)
Another amazing contribution by Lee Sallows:
“The picture above shows a 4×4 geomagic square, which is to say a magic square using geometrical shapes that can be fitted together so as to form an identical target shape, in this case a 4×6 rectangle, rather than numbers adding to a constant sum. In addition, the square is also panmagic, meaning that besides the usual 4 rows, 4 columns, and both main diagonals, the shapes occupying each of the so-called ‘broken’ diagonals, afkn, dejo, cfip, bglm, chin, belo, are also able to tile the rectangle. Lastly, the 4 shapes contained in the corner cells of the four embedded 3×3 sub-squares, acik, bdjl, fhnp, egmo, are also ‘magic’, bringing the total number of target-tiling shape sets to 20, a small improvement over the 16 achieved by a panmagic-only square. With that said, it is worth noting that 4×4 geomagic squares have been found achieving target-tiling scores as high as 48.”
Click the image to expand it. Thanks, Lee!
A disease is spreading rapidly across the country. Half the people who have contracted it have died, and half have recovered on their own. A crash program to ward off the epidemic has produced two serums, A and B, but there’s been little time to test them. All three of the patients who were given serum A recovered, and so did 7 of the 8 patients who were given serum B. Unfortunately, you’ve just learned that you have the disease. If you get no treatment, your chances of surviving are 50-50. Both serums have a better record than that, but which one should you take?
“There doesn’t seem to be anything we can do other than appeal to our intuitive feelings on the matter,” writes University of Waterloo mathematician Ross Honsberger. “However, a very ingenious notion, the so-called ‘null hypothesis,’ permits a measure of analysis which, in this case, yields a definite preference.”
The key is to ask how likely it is that 3 out of 3 patients would have recovered if serum A were neither helping nor hindering them. An untreated patient has a 50-50 chance of recovery, so the answer is
On the other hand, if serum B had no effect, then the chance of 7 recoveries out of 8 is
(Here the factor 8 reflects the fact that there are 8 different possible victims, and again the probability of dying is 1/2.)
So the available evidence suggests that it’s 4 times as likely that serum A has no effect as that serum B has no effect. Your best course is to take serum B.
(Ross Honsberger, “Some Surprises in Probability,” in his Mathematical Plums, 1979.)
The 1968 Putnam Competition included a beautiful one-line proof that π is less than 22/7, its common Diophantine approximation:
The integral must be positive, because the integrand’s denominator is positive and its numerator is the product of two non-negative numbers. But it evaluates to 22/7 – π — and if that expression is positive, then 22/7 must be greater than π.
University of St Andrews mathematician G.M. Phillips wrote, “Who will say that mathematics is devoid of humour?”

In October 2005, Neil Armstrong received a letter from a social studies teacher charging that the moon landings had been faked. “[O]ver 30 years on from the pathetic TV broadcast when you fooled everyone by claiming to have walked upon the Moon,” he wrote, “I would like to point out that you, and the other astronauts, are making yourselfs a worldwide laughing stock … Perhaps you are totally unaware of all the evidence circulating the globe via the Internet. Everyone now knows the whole saga was faked, and the evidence is there for all to see.”
Armstrong replied:
Mr. Whitman,
Your letter expressing doubts based on the skeptics and conspiracy theorists mystifies me.
They would have you believe that the United States Government perpetrated a gigantic fraud on its citizenry. That the 400,000 Americans who worked on an unclassified program are all complicit in the deception, and none broke ranks and admitted their deceit.
If you believe that, why would you contact me, clearly one of those 400,000 liars?
I trust that you, as a teacher, are an educated person. You will know how to contact knowledgeable people who could not have been party to the scam.
The skeptics claim that the Apollo flights did not go to the moon. You could contact the experts from other countries who tracked the flights on radar (Jodrell Bank in England or even the Russian Academicians).
You should contact the Astronomers at Lick Observatory who bounced their laser beam off the Lunar Ranging Reflector minutes after I installed it. Or, if you don’t find them persuasive, you could contact the astronomers at the Pic du Midi observatory in France. They can tell you about all the other astronomers in other countries who are still making measurements from these same mirrors — and you can contact them.
Or you could get on the net and find the researchers in university laboratories around the world who are studying the lunar samples returned on Apollo, some of which have never been found on earth.
But you shouldn’t be asking me, because I am clearly suspect and not believable.
Neil Armstrong
(From James R. Hansen, A Reluctant Icon: Letters to Neil Armstrong, 2020.)

In a 1961 contribution to Analog, Maurice Price explained that, while a new engineer might arrive to a clean desk, a “cycle of confusion” quickly begins as papers pile up so deeply that the engineer can do little more than fish old technical journals from the pile and read them (this is known as “keeping up with the state of the art”). Eventually the engineer resolves to clean the desk, but that only returns the system to the start of the cycle. The key equation is
C = K1 exp (K2t).
“In this equation K1 is the constant of confusion and K2 is the coefficient of chaos. These may vary from desk to desk and from engineer to engineer, but the general form of the curve is not altered. Note that the amount of work to be done does not affect the curve at all. This is because the amount of work expands to overflow the available desk area.”
The only way to break the cycle is to promote the engineer, but that only restarts the cycle at a new desk. And productivity and concentration actually increase with clutter. So the best solution is for the engineer to “bring his desk to the state of stagnation as soon as possible. From then on, the desk should be ignored completely. All work must be carried out by telephone.”
(Maurice Price, “An Introduction to the Calculus of Desk-Clearing,” Analog Science Fact & Fiction, British edition, 1961, 68-72.)