122 + 332 = 1233
882 + 332 = 8833
94122 + 23532 = 94122353
741602 + 437762 = 7416043776
8832122 + 3211682 = 883212321168
Science & Math
Misc
- 2737 = (2 × 7)3 – 7
- Move the C in CABARET and you get A BAR, ETC.
- Van Gogh sold only one painting in his lifetime.
- “He who hesitates is last.” — Mae West
- If a man is convinced he has hypochondria, is he a hypochondriac?
(Thanks, Ben.)
Time Well Spent
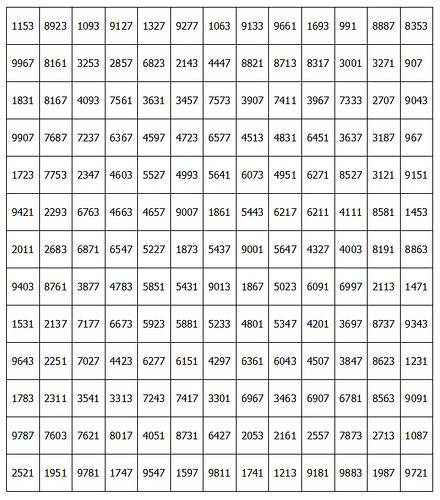
The Journal of Recreational Mathematics published this remarkable magic square, composed by “a puzzlist who at the time was a prison inmate.”
The large 13 × 13 square is magic — that is, each row and column adds to the same sum — but so is each successive nested square, from 11 × 11 down to 3 × 3.
The magic constant of each square is 10,874 smaller than the last.
And every cell is prime.
Cabooses
Square either of these 100-digit numbers and the result will terminate with the original number:
395300731910816980293850989006216650958086381100055742342323089610900
4106619977392256259918212890625
604699268089183019706149010993783349041913618899944257657676910389099
5893380022607743740081787109376
Truncate either one from the left, by any number of digits, and it will retain this property.
Reflections
I’m not sure who originated this — “Hiawatha at Miami,” a tale of auto-repair skulduggery. Composed entirely in letters with left-right symmetry, it was typed with a normal keyboard but must be read in a mirror:
OTTO TUOHTIW OTUA TAHT HTIW
IIAWAH TA AHTAWAIH
–!IXAT A TAHW — IXAT A TIH
.IMAIM TA ATOYOT A
:YVI OT WOV I TUH A TA
.IXAT A TIH AHTAWAIH”
HATU OT TUO TI WOT YAM I
“!YXAW OOT — WOT OT TIAW YAM I
IXAT A HTIW OTTO TUOHTIW
IIAWAH TA AHTAWAIH
-IXAM A — AMIXAM A TIH
!IMAIM TA (OTUA YM) AM
:AVA HTIW TUH A TA MA I
.OTUA YM TIH AHTAWAIH”
.ITIHAT OT TI WOT YAM I
“.OTTO OT TOOT OT TIAW YAM I
AHTAWAIH HTIW YOT YAM I
.OIHO — AWOI TA TUO
IXAT HTOMMAM TAHT WOT YAM I
.UHAO OT — IIAWAH OT
In the same spirit, here’s an equation discovered by Royal V. Heath:
1118 + 1881 + 8181 + 8818 = 1181 + 1818 + 8118 + 8881
Reverse that and you get:
1888 + 8118 + 8181 + 1811 = 8188 + 1818 + 1881 + 8111
Both equations remain true if you square all their terms.
Tupper’s Self-Referential Formula
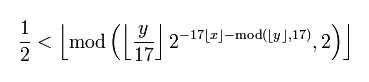
Graph this formula over 0 ≤ x ≤ 106 and k ≤ y ≤ k + 17, with k = 96093937991895888497167
29621278527547150043396601293066515055192717028023952664246896428421743
50718121267153782770623355993237280874144307891325963941337723487857735
74982392662971551717371699516523289053822161240323885586618401323558513
60488286933379024914542292886670810961844960917051834540678277315517054
05381627380967602565625016981482083418783163849115590225610003652351370
34387446184837873723819822484986346503315941005497470059313833922649724
94617515457283667023697454610146559979337985374831437868418065934222278
98388722980000748404719, and you get this:
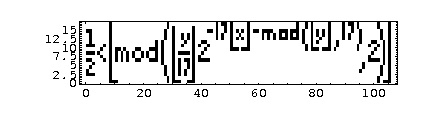
Reasonable enough, right?
Twin Cities

Young Pierre has never left France, but he hears that London is an attractive city. He adopts the belief “Londres est jolie” (“London is pretty”).
Now Pierre’s family moves to another country, whose language he learns directly, without translation into French. He learns that his new city is called London, and eventually forms the belief that “London is not pretty.” He doesn’t know that Londres and “London” refer to the same city.
What are we to make of this? We can’t deny the sincerity of Pierre’s original belief, which he still holds; nor of his new belief; and it seems absurd to claim that he holds both or neither. “Each possibility seems to lead us to say something either plainly false or downright contradictory,” writes Princeton philosopher Saul Kripke. “Yet the possibilities appear to be logically exhaustive.”
“This, then, is the paradox. I have no firm belief as to how to solve it.”
Math Notes
3435= 33 + 44 + 33 + 55
Stops and Starts
Charade sentences devised by Howard Bergerson:
FLAMINGO: PALE, SCENTING A LATENT SHARK! =
FLAMING, OPALESCENT IN GALA TENTS — HARK!
NO! UNCLE-AND-AUNTLESS BE, AS TIES DENY OUR END.
NO UNCLEAN, DAUNTLESS BEASTIES’ DEN YOU REND.
HISS, CARESS PURSUIT, OR ASTOUND, O ROC, O COBRAS!
HIS SCARES SPUR SUITOR, AS TO UNDO ROCOCO BRAS.
HA! THOU TRAGEDY INGRATE, DWELL ON, SUPERB OLD STAG IN GLOOM =
HATH OUTRAGE, DYING, RATED WELL? ON SUPER-BOLD STAGING LOOM!
In the same spirit: 1! 10! 22! 1! = 11! 0! 2! 21!
Faith and Reason

Jean Buridan presented a logical proof of the existence of God:
- God exists.
- Neither of these sentences is true.
The two statements can be reconciled only if God exists.
But see Cloudy, Kangaroo Court, and Powerless.
