Before his students arrived for a graduate course in logic, Raymond Smullyan wrote on the blackboard:
PLEASE DO NOT ERASE — BECAUSE IF YOU DO, THOSE WHO COME LATER WON’T KNOW THAT THEY SHOULDN’T ERASE.
Before his students arrived for a graduate course in logic, Raymond Smullyan wrote on the blackboard:
PLEASE DO NOT ERASE — BECAUSE IF YOU DO, THOSE WHO COME LATER WON’T KNOW THAT THEY SHOULDN’T ERASE.
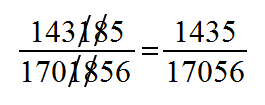

Suppose you flip three fair coins.
Necessarily two will match, and it’s an even chance whether the third will be head or tail.
Therefore the chance that all three will match is 1/2.
8589934592 × 116415321826934814453125 = 1000000000000000000000000000000000
What’s the difference between six dozen dozen and half a dozen dozen?
If you answered “nothing,” reconsider.
Syllogisms offered in Lewis Carroll’s 1896 textbook in symbolic logic:
1. Babies are illogical.
2. Nobody is despised who can manage a crocodile.
3. Illogical persons are despised.
Therefore babies cannot manage crocodiles.
1. No interesting poems are unpopular among people of real taste.
2. No modern poetry is free from affectation.
3. All your poems are on the subject of soap bubbles.
4. No affected poetry is popular among people of taste.
5. Only a modern poem would be on the subject of soap bubbles.
Therefore all your poems are uninteresting.
Raymond Smullyan proposes a scene in which two men are regarding a blackboard. On the board is written ONLY AN IDIOT WOULD BELIEVE THIS SENTENCE.
The first man says, “Do you believe that sentence?”
The second says, “Of course not. Only an idiot would believe that sentence.”
“He clearly does believe it, yet he says he doesn’t believe it,” Smullyan says. “So he’s in the curious position of believing something and also believing that he doesn’t believe it.”
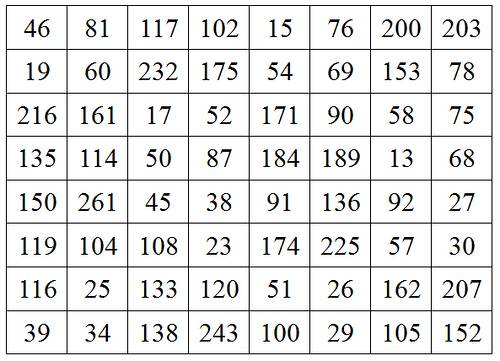
A doubly magic square: Every row and column adds to 840 and multiplies to 2,058,068,231,856,000.
The waistcoat should first be unbuttoned in the front, and then the buckle at the back must be unloosed. The operator, standing in front of the person operated upon, should then place his hands underneath the coat at the back, taking hold of the bottom of the waistcoat, at the same time requesting the wearer to extend his arms at full length over his head. Now raise the bottom part of the waistcoat over the head of the wearer (if the waistcoat be tight it will be necessary to force it a little, but this must not be minded so long as the waistcoat is not torn); the waistcoat then will have been brought to the front of the wearer, across his chest. Take the right side bottom-end of the waistcoat, and put it into the arm-hole of the coat at the shoulder, at the same time putting the hand up the sleeve, seizing the end, and drawing it down the sleeve; this action will release one arm-hole of the garment to be removed. The next thing to be done is to pull the waistcoat back again out of the sleeve of the coat, and put the same end of the waistcoat into the left arm-hole of the coat, again putting the hand up the sleeve of the coat as before, and seizing the end of the garment. It may then be drawn quite through the sleeve, and the puzzle is accomplished.
— Cassell’s Complete Book of Sports and Pastimes, 1896

In 1610, thinking he had discovered two moons orbiting Saturn, Galileo composed a message:
ALTISSIMUM PLANETAM TERGEMINUM OBSERVAVI (“I have observed the most distant planet to have a triple form”)
… and sent it to Kepler as an anagram:
SMAISMRMILMEPOETALEUMIBUNENUGTTAUIRAS
Remarkably, Kepler managed to “solve” this as a message about Mars, not Saturn:
SALVE UMBISTENEUM GEMINATUM MARTIA PROLES (“Hail, twin companionship, children of Mars”)
The German astronomer had predicted that the Red Planet had two moons, and imagined that Galileo was confirming his belief.
There’s a message in this, somewhere.