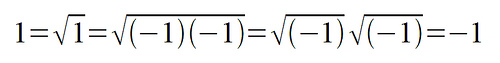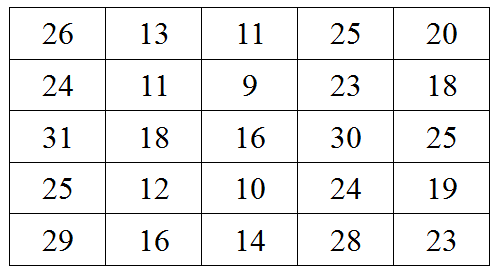
Pick any number in this array and cross off all the other numbers in its row and column. Repeat this four more times, after which no more numbers will be available.
Add your five numbers. If they total exactly 100, you must rob 10 banks and pass the money to me through a series of prearranged drops. Contact me for details.