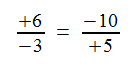1/998001 = 0.000001002003004005006007008009010011012013014015016017018019020 0210220230240250260270280290300310320330340350360370380390400410420430440450 4604704804905005105205305405505605705805906006106206306406506606706806907007 1072073074075076077078079080081082083084085086087088089090091092093094095096 0970980991001011021031041051061071081091101111121131141151161171181191201211 2212312412512612712812913013113213313413513613713813914014114214314414514614 7148149150151152153154155156157158159160161162163164165166167168169170171172 1731741751761771781791801811821831841851861871881891901911921931941951961971 9819920020120220320420520620720820921021121221321421521621721821922022122222 3224225226227228229230231232233234235236237238239240241242243244245246247248 2492502512522532542552562572582592602612622632642652662672682692702712722732 7427527627727827928028128228328428528628728828929029129229329429529629729829 9300301302303304305306307308309310311312313314315316317318319320321322323324 3253263273283293303313323333343353363373383393403413423433443453463473483493 5035135235335435535635735835936036136236336436536636736836937037137237337437 5376377378379380381382383384385386387388389390391392393394395396397398399400 4014024034044054064074084094104114124134144154164174184194204214224234244254 2642742842943043143243343443543643743843944044144244344444544644744844945045 1452453454455456457458459460461462463464465466467468469470471472473474475476 4774784794804814824834844854864874884894904914924934944954964974984995005015 0250350450550650750850951051151251351451551651751851952052152252352452552652 7528529530531532533534535536537538539540541542543544545546547548549550551552 5535545555565575585595605615625635645655665675685695705715725735745755765775 7857958058158258358458558658758858959059159259359459559659759859960060160260 3604605606607608609610611612613614615616617618619620621622623624625626627628 6296306316326336346356366376386396406416426436446456466476486496506516526536 5465565665765865966066166266366466566666766866967067167267367467567667767867 9680681682683684685686687688689690691692693694695696697698699700701702703704 7057067077087097107117127137147157167177187197207217227237247257267277287297 3073173273373473573673773873974074174274374474574674774874975075175275375475 5756757758759760761762763764765766767768769770771772773774775776777778779780 7817827837847857867877887897907917927937947957967977987998008018028038048058 0680780880981081181281381481581681781881982082182282382482582682782882983083 1832833834835836837838839840841842843844845846847848849850851852853854855856 8578588598608618628638648658668678688698708718728738748758768778788798808818 8288388488588688788888989089189289389489589689789889990090190290390490590690 7908909910911912913914915916917918919920921922923924925926927928929930931932 9339349359369379389399409419429439449459469479489499509519529539549559569579 5895996096196296396496596696796896997097197297397497597697797897998098198298 3984985986987988989990991992993994995996997999 ...
(Thanks, William.)