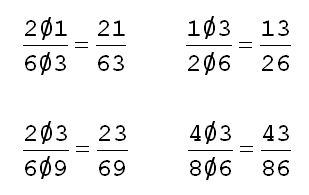In 1921, chemists at Arthur D. Little Inc. reduced 100 pounds of sows’ ears to glue, converted it to gelatin, forced it into fine strands, and wove these into a purse “of the sort which ladies of great estate carried in medieval days — their gold coin in one end and their silver coin in the other.”
“We made this silk purse from a sow’s ear because we wanted to, because it might serve as an example to clients who come to us with their ambitions or their troubles, and also as a contribution to philosophy,” they reported. “Things that everybody thinks he knows only because he has learned the words that say it, are poisons to progress.”