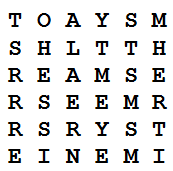The knight’s tour is a familiar task in chess: On a bare board, find a path by which a knight visits each of the 64 squares exactly once. There are many solutions, but finding them by hand can be tricky — the knight tends to get stuck in a backwater, surrounding by squares that it’s already visited. In 1823 H.C. von Warnsdorff suggested a simple rule: Always move the knight to a square from which it will have the fewest available subsequent moves.
This turns out to be remarkably effective: It produces a successful tour more than 85% of the time on boards smaller than 50×50, and more than 50% of the time on boards smaller than 100×100. (Strangely, on a 7×7 board its success rate drops to 75%; see this paper.) The video above shows a successful tour on a standard chessboard; here’s another on a 14×14 board:
While we’re at it: British puzzle expert Henry Dudeney once set himself the task of devising a complete knight’s tour of a cube each of whose sides is a chessboard. He came up with this:
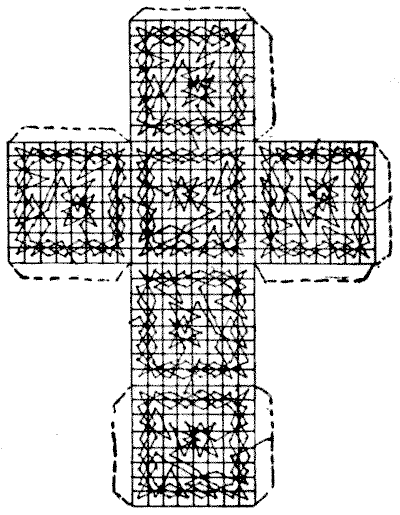
If you cut out the figure, fold it into a cube and fasten it using the tabs provided, you’ll have a map of the knight’s path. It can start anywhere and make its way around the whole cube, visiting each of the 364 squares once and returning to its starting point.
Dudeney also came up with this puzzle. The square below contains 36 letters. Exchange each letter once with a letter that’s connected with it by a knight’s move so that you produce a word square — a square whose first row and first column comprise the same six-letter word, as do the second row and second column, and so on.
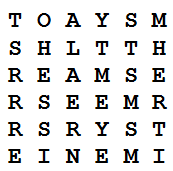
So, for example, starting with the top row you might exchange T with E, O with R, A with M, and so on. “A little thought will greatly simplify the task,” Dudeney writes. “Thus, as there is only one O, one L, and one N, these must clearly be transferred to the diagonal from the top left-hand corner to the bottom right-hand corner. Then, as the letters in the first row must be the same as in the first file, in the second row as in the second file, and so on, you are generally limited in your choice of making a pair. The puzzle can therefore be solved in a very few minutes.”