In a standard 10-frame game of bowling, the lowest possible score is 0 (all gutterballs) and the highest is 300 (all strikes). An average player falls somewhere between these extremes. In 1985, Central Missouri State University mathematicians Curtis Cooper and Robert Kennedy wondered what the game’s theoretical average score is — if you compiled the score sheets for every legally possible game of bowling, what would be the arithmetic mean of the scores?

It turns out it’s pretty low. There are (66⁹)(241) possible games, which is about 5.7 × 10¹⁸. If we divide that into the total number of points scored in these games, we get

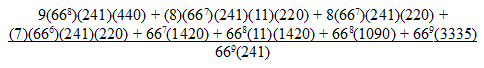
which is about 80 (79.7439 …).

This “might make you feel better about your average,” Cooper and Kennedy conclude. “The mean bowling score is indeed awful even if you are just an occasional bowler. Even though this information is interesting, there are more difficult questions about the game of bowling that could be asked. For example, you might wish to determine the standard deviation of the set of bowling scores and hence know more about the distribution of the set of all bowling scores. But the exact determination of the distibution of the set of scores is, in our opinion, a difficult problem. For example, given an integer k between 0 and 300, how many different bowling games have the score k? This, we leave as an open problem.”

(Curtis N. Cooper and Robert E. Kennedy, “Is the Mean Bowling Score Awful?”, Journal of Recreational Mathematics 18:3, 1985-86.)