A curious puzzle from the Penguin Problems Book, 1940:
A certain number consisting entirely of 7s is divisible by 199. Find the last four digits of the quotient, without finding the entire quotient.
A curious puzzle from the Penguin Problems Book, 1940:
A certain number consisting entirely of 7s is divisible by 199. Find the last four digits of the quotient, without finding the entire quotient.
A puzzle by Frank Morgan: The meaning of a common English word becomes plural when an A is added at its start. What is the word?

A puzzle by MIT mathematician Tanya Khovanova:
Three logicians walk into a bar. Each is wearing a hat that’s either red or blue. Each logician knows that the hats were drawn from a set of three red and two blue hats; she doesn’t know the color of her own hat but can see those of her companions.
The waiter asks, “Do you know the color of your own hat?”
The first logician answers, “I do not know.”
The second logician answers, “I do not know.”
The third logician answers, “Yes.”
What is the color of the third logician’s hat?
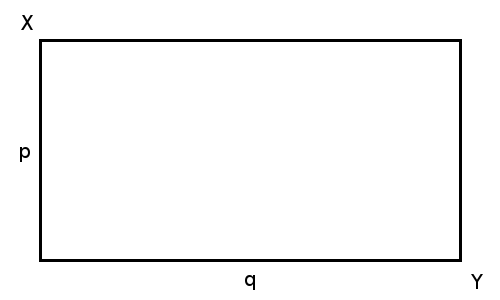
Richard Hess posed this problem in the Spring 1980 issue of Pi Mu Epsilon Journal. At noon on Monday, a bug departs the upper left corner, X, of a p × q rectangle and crawls within the rectangle to the diagonally opposite corner, Y, arriving there at 6 p.m. He sleeps there until noon on Tuesday, when he sets out again for X, crawling along another path within the rectangle and reaching X at 6 p.m. Prove that at some time on Tuesday the bug was no farther than p from his location at the same time on Monday.

During a visit to Crete in 1938, Miss L.S. Sutherland described a game she saw played on a pentagram:
You have nine pebbles, and the aim is to get each on one of the ten spots. You put your pebble on any unoccupied spot, saying ‘one’, and then move it through another, ‘two’, whether this spot is occupied or not, to a third, ‘three’, which must be unoccupied when you reach it; these three spots must be in a straight line. If you know the trick, you can do this one-two-three trick, for each of your nine pebbles and find it a berth, and then you win your money. If you don’t know the trick, it’s extremely hard to do it.
To make this a bit clearer: The figure has 10 “spots,” the five points of the star and the five corners of the pentagon in the middle. A move consists of putting a pebble on any unoccupied spot, moving it through an adjacent spot (which may be occupied) and continuing in a straight line to the next adjacent spot, which must be unoccupied. You then leave the pebble there and start again with a new pebble, choosing any unoccupied spot to begin this next move. If you can fill 9 of the 10 spots in this way then you’ve won.
Can you find a solution?

By T.R. Dawson. “The problem is for each White man to capture the corresponding Black man in such a way that the routes traversed by each man never come in contact with one another.”

For four months in 1840 Edgar Allan Poe conducted a puzzle column for the Philadelphia newspaper Alexander’s Daily Messenger. In that time he defied his readers to send him a cryptogram that he could not solve, and at the end of his tenure he declared himself undefeated. One of the later challenges came from 17-year-old Schuyler Colfax of New Carlisle, Iowa, who would grow up to become vice president of the United States:
Dear Sir — As you have in your Weekly Messenger defied the world to puzzle you by substituting arbitrary signs, figures, etc. for the different letters of the alphabet, I have resolved to try my utmost to corner you and your system together, and have manufactured the two odd looking subjects which accompany this as avant couriers. … If you succeed in solving the accompanying, I will, of course, as you request, acknowledge it publicly to my friends.
Poe responded: “We have only time, this week, to look at the first and longest cypher — the unriddling of which, however, will no doubt fully satisfy Mr. Colfax that we have not been playing possum with our readers.” Here’s Colfax’s cryptogram:
8n()58†d w!0 b† !x6n†z k65 !nz k65,8l†n b)x 8nd)Pxd !zw8x 6k n6 36w-†nd!x86n;
x=†0 z†,5!z† x=† w8nz 8n 8xd 62n †dx††w !nz k653† 8x x6 5†36l†5 8xd P†l†P b0 5†l†n,†.
()n8)d
What’s the solution?

A problem by Wayne M. Delia and Bernadette D. Barnes:
Five children — Ivan, Sylvia, Ernie, Dennis, and Linda — entered a candy store, and one of them stole a box of candy from the shelf. Afterward each child made three statements:
Ivan:
1. I didn’t take the box of candy.
2. I have never stolen anything.
3. Dennis did it.
Sylvia:
4. I didn’t take the box of candy.
5. I’m rich and I can buy my own candy.
6. Linda knows who the crook is.
Ernie:
7. I didn’t take the box of candy.
8. I didn’t know Linda until this year.
9. Dennis did it.
Dennis:
10. I didn’t take the box of candy.
11. Linda did it.
12. Ivan is lying when he says I stole the candy.
Linda:
13. I didn’t take the box of candy.
14. Sylvia is guilty.
15. Ernie can vouch for me, because he has known me since I was a baby eight years ago.
If each child made two true and one false statement, who stole the candy?
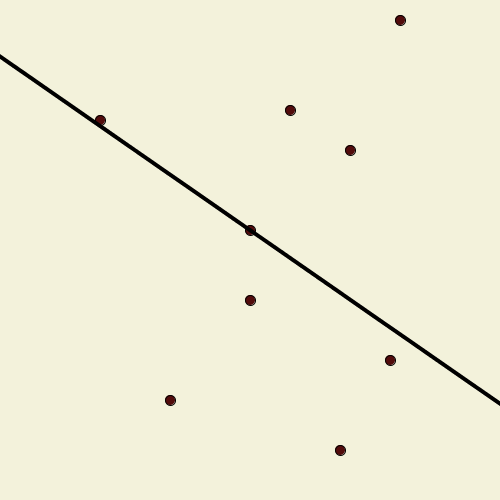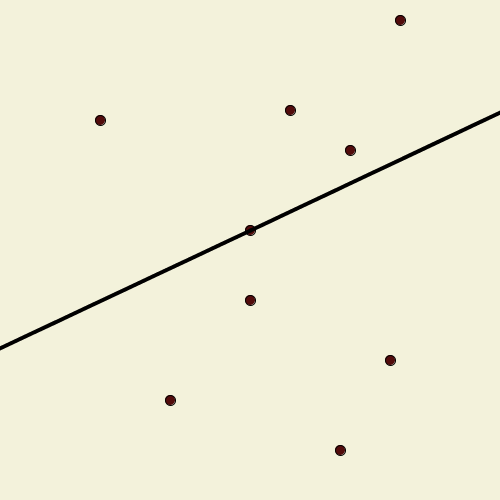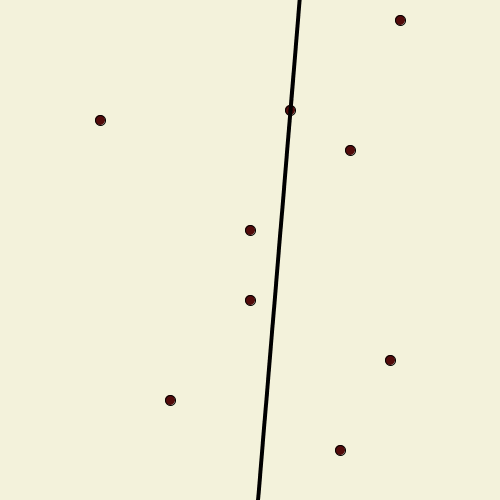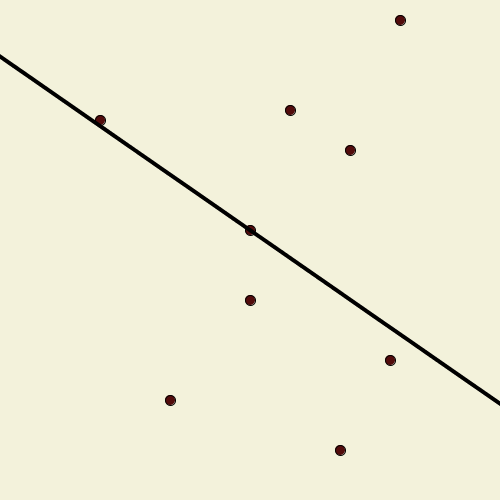
Suppose we have a finite set of points in the plane, no three of which are collinear. A line drawn through one of them pivots around that point until it encounters another point, when it adopts that point as the new pivot. Call this line a “windmill”; it continues indefinitely, always rotating in the same direction. Show that we can choose an initial point and line so that the resulting windmill uses each point as a pivot infinitely many times.