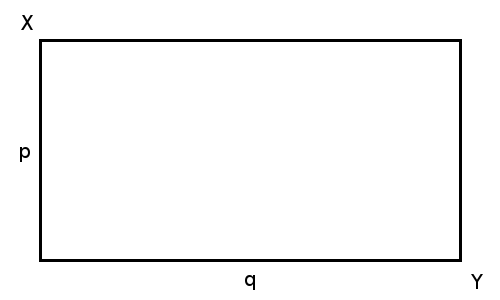
Richard Hess posed this problem in the Spring 1980 issue of Pi Mu Epsilon Journal. At noon on Monday, a bug departs the upper left corner, X, of a p × q rectangle and crawls within the rectangle to the diagonally opposite corner, Y, arriving there at 6 p.m. He sleeps there until noon on Tuesday, when he sets out again for X, crawling along another path within the rectangle and reaching X at 6 p.m. Prove that at some time on Tuesday the bug was no farther than p from his location at the same time on Monday.
|
SelectClick for Answer |
Well, suppose there are two bugs making their journeys simultaneously — one departs X as the other departs Y, each headed for the opposite corner, and they travel different paths within the rectangle, arriving at their destinations simultaneously. At some time during their journeys they’ll both be the same horizontal distance from the left side of the rectangle. Since both paths remain within the rectangle, at that moment the distance between them can’t be greater than p.
The editors received this answer from six readers, including Hess. “Their solutions were characterized by the complete absence of mathematical symbols and mathematical jargon,” they noted. “While there is certainly no objection to mathematical solutions to mathematical problems, a simple word-solution intelligible to any layman is to be preferred. Some of the other submitted solutions were profuse with subscripts, coordinates, inequalities, vinculi, functional relations, intermediate value theorems, Greek symbols, graphs, continuous functions and derivatives — all reminiscent of the sledgehammer method of swatting a fly.”
The original problem is here (PDF, page 135).
|

