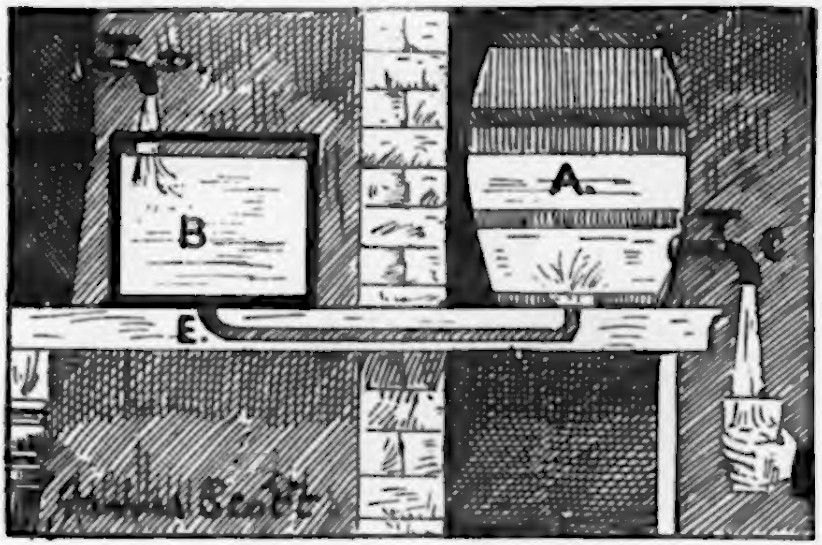
In 1895 a London shopkeeper attracted customers with a glass cask of whiskey — they were puzzled to find that no matter how much liquid they drew off, the level in the cask never dropped. The container could be viewed from any angle, and it stood well away from the wall. How was this possible?
A hidden pipe connected the bottom of the cask to a tank in another room. When a customer drew a glass of whisky, a confederate there would open a tap to replenish tank B, and the liquid, seeking its own level, would maintain the same height in the cask.
(James Scott, “Shopkeepers’ Advertising Novelties,” Strand, November 1895. See Desert Downpour.)