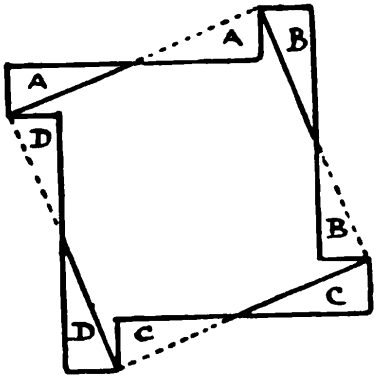
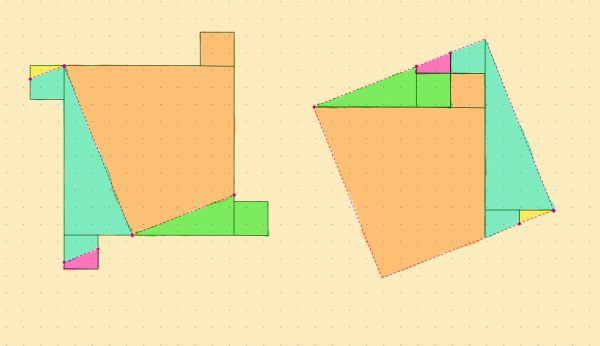
A conference is attended by 1,000 delegates from various countries. It’s known that any three delegates can speak together without help, though one of the three may have to serve as interpreter for the other two. Prove that all the attendees can be accommodated in double rooms so that the two occupants of each room can speak to each other.
Puzzles
Straightforward
D.C.B. Marsh proposed this problem in the American Mathematical Monthly in 1957:
“Solve a3 – b3 – c3 = 3abc, a2 = 2(b + c) simultaneously in positive integers.”
There are a number of ways to go about this, but Raymond Huck of Marietta College found a strikingly simple one. 3abc is positive, so the first equation tells us immediately that b < a and c < a. Add these two facts together and we get b + c < 2a, and hence 2(b + c) < 4a. Substituting this conveniently into the second equation, we learn that a2 < 4a and a < 4. The second equation also shows that a is an even number, so a must be 2, and b and c, which are smaller, must both be 1.
(“Solutions,” American Mathematical Monthly 65:1 [January 1958], 43-46, Problem E1266, via Ross Honsberger, Mathematical Morsels, 1979.)
Helmet Crash
A problem proposed by Mel Stover for the April 1953 issue of Pi Mu Epsilon Journal:
After a meeting of six professors, each man left with another’s hat. The hat that Aitkins took belonged to the man who took Baily’s hat. The man whose hat was taken by Caldwell took the hat of the man who took Dunlop’s hat. And the man who took Easton’s hat wasn’t the one whose hat was taken by Fort. Who took Aitkins’ hat?
Simple Enough
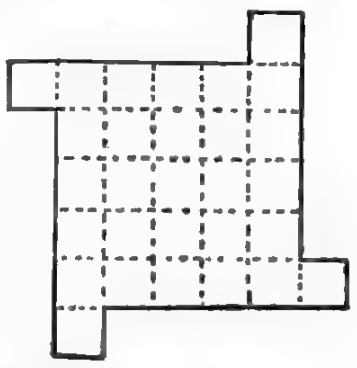
“It often happens that the easiest dissection puzzles are the prettiest,” wrote Henry Dudeney in 1914. “Here is a new one that ought to give the reader very little trouble. Cut the figure into five pieces that will fit together and form a square.”
An Odd Request

A puzzle by Polish mathematician Paul Vaderlind:
Is it possible to arrange 25 whole numbers (not necessarily all different) so that the sum of any three successive terms is even but the sum of all 25 is odd?
The King’s Salary
A little kingdom contains 66 people, a king and 65 citizens. Each of them, including the king, has a salary of one gold piece. When democracy comes, the king is denied a vote, but he has the power to suggest changes, in particular regarding the redistribution of salaries. The salaries must total 66, and each salary must be a whole number of gold pieces. The citizens will vote on each suggestion, which will pass if more citizens vote for it than against it. Each voter will reliably support a measure if it will increase his salary, oppose it if it will decrease his salary, and otherwise abstain from voting.
The king is greedy. What’s the highest salary he can arrange for himself?
Inside Job

Here’s a unit square. Prove that, if nine points are identified in the square’s interior, we can always find three of them that form a triangle of area 1/8 or less.
Mirror Numbers
A puzzle by A. Vasin from the July-August 1993 issue of Quantum:
Two numbers are mirror numbers if each presents the digits of the other in reverse order, such as 123 and 321. Find two mirror numbers whose product is 92,565.
Leapfrog
A puzzle by Y. Ionin, from the September/October 1990 issue of Quantum:
Three frogs occupy three vertices of a square. When one frog jumps over another, it lands beyond it at the same distance that had originally separated them. Can any frog reach the fourth vertex?
Javelin
A puzzle by Steven T., a systems engineer at the National Security Agency, from the NSA’s September 2016 Puzzle Periodical:
Three athletes (and only three athletes) participate in a series of track and field events. Points are awarded for 1st, 2nd, and 3rd place in each event (the same points for each event, i.e. 1st always gets “x” points, 2nd always gets “y” points, 3rd always gets “z” points), with x > y > z > 0, and all point values being integers.
The athletes are named Adam, Bob, and Charlie.
- Adam finished first overall with 22 points.
- Bob won the Javelin event and finished with 9 points overall.
- Charlie also finished with 9 points overall.
Question: Who finished second in the 100-meter dash (and why)?