
Black is clearly lost. But there are two squares on which his king can never be checkmated, even if White is allowed to make consecutive moves and checks are ignored. What are they?

Black is clearly lost. But there are two squares on which his king can never be checkmated, even if White is allowed to make consecutive moves and checks are ignored. What are they?

A problem from Sam Loyd’s Cyclopedia of Puzzles, 1914:
Here is the puzzle of Tom the Piper’s Son, who, as told by ‘Mother Goose,’ stole the pig and away he run. It is known that Tom entered the far gate shown at the top on the right hand. The pig was rooting at the base of the tree 250 yards distant, and Tom captured it by always running directly towards it, while the pig made a bee-line towards the lower corner as shown. Now, assuming that Tom ran one-third faster than the pig, how far did the pig run before he was caught?
Intriguingly, Loyd adds, “The puzzle is a remarkable one on account of its apparent simplicity and yet the ordinary manner of handling problems of this character is so complicated that solvers are asked merely to submit approximately correct answers, based upon judgment and common sense, just to see who can make the best guess. The simple rule for solving it, however, which will doubtless be quite new to our puzzlists, is based upon elementary arithmetic.” What’s the answer?

In 1915 James Ferguson Smyth invited Hermann Helms to play a practice game at the Manhattan Chess Club. They had reached the position above when Helms, as Black, found a brilliant two-move mate. What is it?
A problem from the 1999 Russian Mathematical Olympiad:
Each cell of a 50×50 square is colored in one of four colors. Show that there exists a square which has cells of the same color as it directly above, directly below, directly to the left, and directly to the right of it (though not necessarily adjacent to it).
An old problem from the Soviet Mathematical Olympiad:
Find the 4-digit number aabb that is a perfect square.
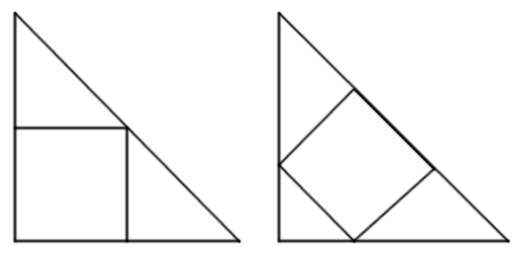
A square has been inscribed in each of two congruent isosceles right triangles. Which square is larger?

This problem, by V. Tchepizhni, won fifth prize in the Bohemian Centenary Tourney of 1962. It’s four puzzles in one:
(a) The diagrammed position.
(b) Turn the board 90 degrees clockwise.
(c) Turn the board 180 degrees.
(d) Turn the board 270 degrees clockwise.
Each of the resulting positions presents a helpmate in two: Black moves first, then White, then Black, then White, the two sides cooperating to reach a position in which Black is checkmated. What are the solutions?
A puzzle by Ezra Brown and James Tanton:
Three gnomes sit in a circle. An evil villain puts a hat on each gnome’s head. Each hat is either rouge or puce, the color chosen by the toss of a coin. Each gnome can see the color of his companions’ hats but not of his own.
At the villain’s signal, all three gnomes must speak at once, each either guessing the color of his own hat or saying “Pass.” If at least one of them guesses correctly and none guesses incorrectly, all three gnomes will live. But if any of them guesses incorrectly, or if all three pass, they’ll all die.
They may not communicate in any way during the game, but they can confer beforehand. How can they arrange a 75 percent chance that they’ll survive?
A puzzle from MIT Technology Review, September-October 1999: A popular pastime at Bell Labs in the 1970s was to identify a word that contains a given string of letters — for example, OOKKEE is found in BOOKKEEPER. Michael Foster found English words that contain HIPE, HCR, and UFA. What are they?