
Here are six new lateral thinking puzzles — play along with us as we try to untangle some perplexing situations using yes-or-no questions.

Here are six new lateral thinking puzzles — play along with us as we try to untangle some perplexing situations using yes-or-no questions.
Jonathan Swift’s Journal to Stella, a collection of 65 letters written to his friend Esther Johnson, contains some puzzling passages, such as this one:
“He gave me al bsadnuk lboinlpl dfaonr ufainfbtoy dpionufnad, which I sent him again by Mr. Lewis.”
How should the obscured phrase be read?
Areas from r/blackmagicfuckery
An interesting problem from Crux Mathematicorum, March 2004: The increasing sequence 1, 5, 6, 25, 26, 30, 31, 125, 126, … consists of positive integers that can be formed by adding distinct powers of 5. That is, 1 = 50, 5 = 51, 6 = 50 + 51, and so on. What’s the 75th integer in this sequence?
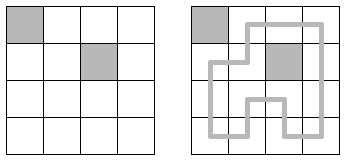
Puzzle maven Nob Yoshigahara offered this puzzle in the September-October 2000 issue of MIT Technology Review, attributing it to a Professor Kotani. In the 4 × 4 complex of rooms above, two of the rooms are closed. This leaves a single way to tour the remaining rooms in a series of orthogonal moves, visiting each room once and returning to the starting point.
The 12 × 12 complex below has a similarly unique solution. What is it?


Luigi Ceriani published this curiously ambivalent retrograde puzzle in Europe Echecs in 1960. White is to mate in two moves.
The answer turns on whether White can castle kingside and whether Black can castle queenside. Castling is always deemed to be legal unless it can be proven otherwise. The question of White’s castling comes down to the origin of the rook on a6. If that started on h1, then White may not castle because the rook that’s currently on h1 obviously must have moved in order to get there. If the rook on a6 started on a1, then again White may not castle, because in that case the rook must have got to its present position via e1, since the pawn originally on a2 can have reached its present position on b3 only after the knight on a1 had itself moved there from b3.
That means that if the rook on a6 is not a promoted piece, White cannot castle. If it is a promoted piece, then Black cannot castle, because the white pawn that was promoted must have passed over either d7 or f7 first, which would have forced the black king to move if it had been on its original square. Hence either castling by White or castling by Black is impossible.
Well, if castling by Black is impossible, then White can win by castling himself, since then Black has no escape from 2. Rf8#. And if castling by White is impossible, then White can capture the b5 pawn en passant (followed by mate with the queen), because if Black’s king and rook have not moved then Black’s last move must have been b7-b5. (His last move cannot have been b6-b5 because that would leave White no possible previous move. As it is, with Black’s last move being b7-b5, White’s preceding move must have been R[c6]xa6+.)
(Via John M. Rice, An ABC of Chess Problems, 1970.) (Maybe I’m being obtuse, but isn’t it possible that neither side can castle? In that case both proposed mates fall apart and I don’t see how White can succeed.)
02/03/2020 UPDATE: Ach, I’d just given the answer to my own question: Castling is deemed to be legal unless it can be proven otherwise, and it can’t be proven that neither side can castle. (Thanks, David and Daniel.)
Reader Jack McLachlan found this curious entry among the marriage notices in the Scots Magazine of January 1790:
At Newburn, near Newcastle, Mr William Dormand, to Miss Hannah Hoy, of that place. The ceremony was attended by the father, mother, brother, sister, aunt, nephew, two husbands, and two wives, and yet there were only four persons present at the marriage.
No explanation is given. How is such an arrangement possible?