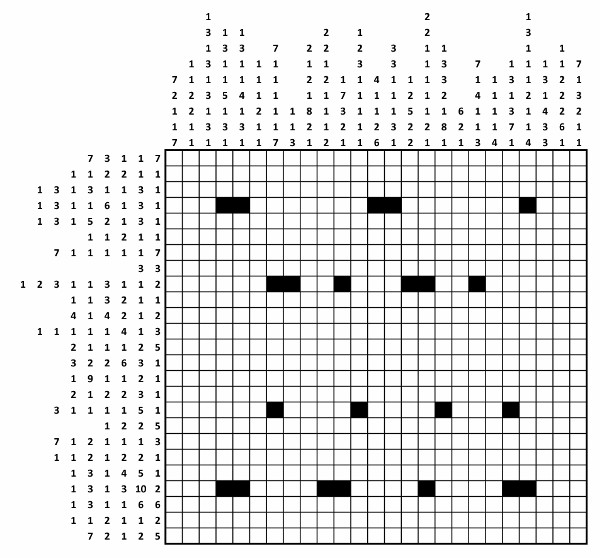
A problem by Atlantic College mathematician Paul Belcher:
Anna and Bert invite n other couples to a dinner party. Before the meal begins, some people shake hands. No one shakes hands with their own partner, no one shakes hands with themselves, and no two people shake hands with each other more than once. Afterward, Anna asks all the other 2n + 1 people how many times they shook hands, and she gets a different answer from each of them. How many times did Anna shake hands?