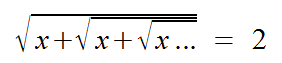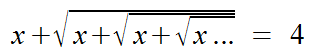Puzzles
Emptied Nest
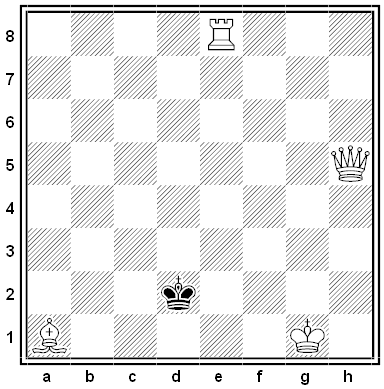
Black and White
Short-Handed
Suppose we have a clock whose hour and minute hands are identical. How times times per day will we find it impossible to tell the time, provided we always know whether it’s a.m. or p.m.?
Ice Water
A boat floats in a swimming pool. In the boat is a block of ice. If the block is dumped into the water and melts, does the water level rise or fall?
The Broken Deck
When eight certain cards are removed from a standard poker deck, it becomes impossible to deal a straight flush. What are the cards? (Assume the deck contains no jokers.)
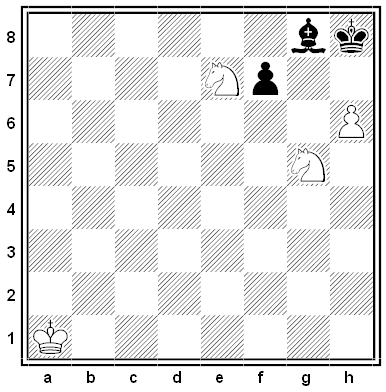
Black and White
Bootstrap Percolation

On a 12 × 12 grid, some squares are infected and some are healthy. On each turn, a healthy square becomes infected if it has two or more infected orthogonal neighbors. (In the example above, the black squares are infected, the white squares are healthy, and the gray squares will be infected next turn.) What’s the smallest number of initially infected squares that can spread an infection over the whole board?
Counterfeit Redux
A more challenging version of the Counterfeit Coin puzzle from 2011:
You have 12 coins, one of which has been replaced with a counterfeit. The false coin differs in weight from the true ones, but you don’t know whether it’s heavier or lighter. How can find it using three weighings in a pan balance?
“A Financial Puzzle”
This, now, is straightforward and business-like: A. applied to B. for a loan of $100. B. replied, ‘My dear A., nothing would please me more than to oblige you, and I’ll do it. I haven’t $100 by me, but make a note and I’ll indorse it, and you can get the money from the bank.’ A. proceeded to write the note. ‘Stay,’ said B., ‘make it $200. I want $100 myself.’ A. did so, B. indorsed the paper, the bank discounted it, and the money was divided. When the note became due, B. was in California, and A. had to meet the payment. What he is unable to cipher out is whether he borrowed $100 of B., or B. borrowed $100 of him.
— Henry C. Percy, Our Cashier’s Scrap-Book, 1879