Puzzles
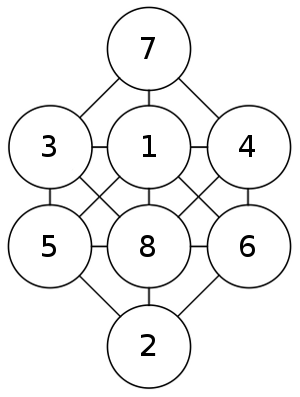
Digit Jump
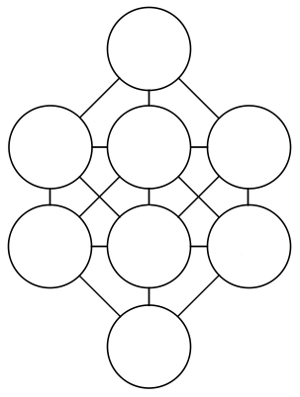
Place the digits 1 through 8 into these circles so that no two successive numbers are connected by a line. If we don’t count rotations or reflections, the solution is unique.
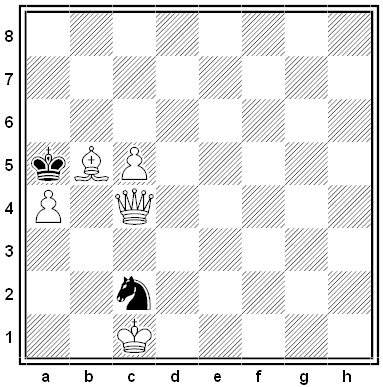
Black and White
Misterioso
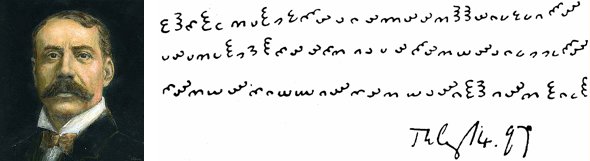
Edward Elgar loved hidden meanings. The English composer filled his letters with wordplay and musical riddles, and he named one of his family homes Craeg Lea, an anagram of the names (C)arice (A)lice and (E)dward ELGAR.
Two of his puzzles have never been solved. One lies at the heart of the so-called Enigma variations, a set of 14 variations on a theme that Elgar said is “not played.” What does this mean? “The Enigma I will not explain,” he wrote in a program note for the first performance in 1899. “Its ‘dark saying’ must be left unguessed, and I warn you that the connection between the Variations and the Theme is often of the slightest texture; further, through and over the whole set another and larger theme ‘goes’, but is not played. … So the principal Theme never appears, even as in some late dramas … the chief character is never on the stage.” He took the solution to his grave, and music lovers have been searching for the hidden theme for more than 100 years.
The second mystery lies in a letter that Elgar wrote two years before Enigma premiered. On July 14, 1897, he sent the message above to 22-year-old Dora Penny, the daughter of his close friend Alfred Penny, rector of St. Peter’s, Wolverhampton. “It is well known that Elgar was always interested in puzzles, ciphers, cryptograms, and the like,” she wrote in her book Edward Elgar: Memories of a Variation. “The cipher here reproduced — the third letter I had from him, if indeed it is one — came to me enclosed in a letter from [Elgar’s wife] to my stepmother. On the back of it is written ‘Miss Penny.’ It followed upon their visit to us at Wolverhampton in July 1897. I have never had the slightest idea what message it conveys; he never explained it and all attempts to solve it have failed. Should any reader of this book succeed in arriving at a solution it would interest me very much to hear of it.”
No satisfactory solution has ever been found. Elgar named Dora herself as the inspiration for the 10th variation of the Enigma, so some wonder whether this was a clue. When she asked him in later life about the musical puzzle, he said, “I thought you, of all people, would guess it.” But no one knows what this means, and if Dora ever found the answer she told no one before her death in 1964. Perhaps the solution is now beyond our reach.
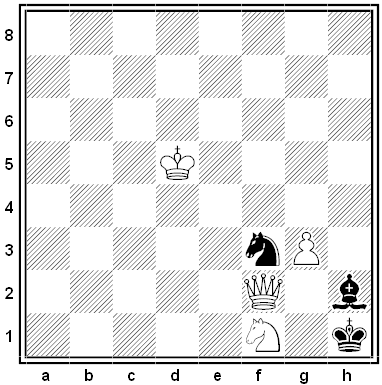
Black and White
Blowin’ in the Wind
You’re taking care of a friend’s house while he’s on vacation. One hot day you pull the chain on a ceiling fan, and when it doesn’t respond you realize the house has temporarily lost power. Unfortunately, you have to leave now, and you’ll be away for several days.
You know that the fan was in the “off” position before you pulled the chain, and that pulling the chain successively will cycle it through its remaining settings (“off,” “high,” “medium,” etc.). You don’t know how many settings there are, but you’re sure there aren’t more than 4.
How can you ensure that the fan will be in the “off” position when power is restored? (Assume that you can’t simply cut the fan’s power.)
Hat Check
One hundred people stand in a line, all facing in the same direction. Each is wearing a red or a blue hat, assigned at random. Each person can see all the hats before him in the line, but not his own or those of the people behind him. Starting at the back of the line, each person in turn must guess the color of his own hat. Each person can hear all the prior guesses. If the group are allowed to discuss strategy beforehand, how many can be sure of guessing correctly?
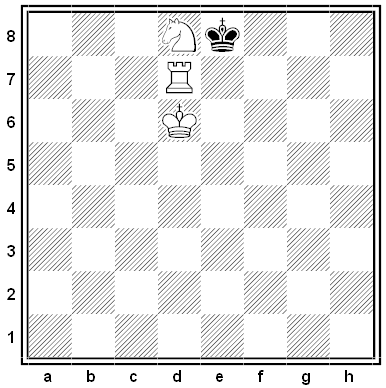
Black and White
A Letter Home
Young telegraph operator Joseph Orton Kerbey was enlisted as a spy for the federal forces during the Civil War. In 1861, laid up in a sick bed in Richmond, he needed a way to communicate his latest discoveries to his friends in the north. The message would have to appear innocent and contain the key to its own decipherment. Here’s what he sent:

He directed it, not to his father’s name and address, but to a friend in the telegraph office at Annapolis. What was the hidden message?
20 to 3

Prove that, if we choose nine vertices of a regular icosagon, some three of these will form an isosceles triangle.