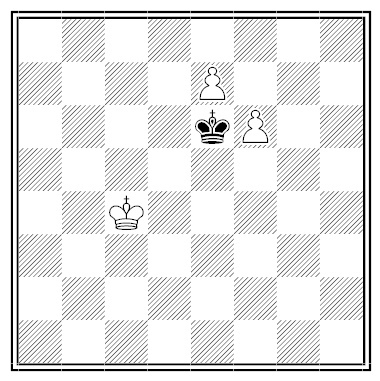
By Bruno Sommer, 1910. White has just moved, and he realizes too late that he could have mated Black on the move. What was his last move, and what was the mate?

By Bruno Sommer, 1910. White has just moved, and he realizes too late that he could have mated Black on the move. What was his last move, and what was the mate?
A family of four has to cross a river. The father and mother each weigh 150 pounds, and each of the two sons weighs 75 pounds. Unfortunately, the boat will carry only 150 pounds maximum. How can they get across?
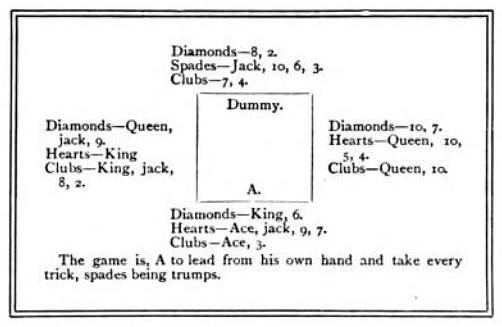
I don’t play bridge, so I’m posting this somewhat blindly. It was devised by W.H. Whitfeld, card editor of the Field, apparently in the late 19th century. The reader who submitted it to the Strand wrote, “If you don’t know the solution, I guarantee that it will take you or any of your staff three or four days.”
“We have a higher opinion of our readers’ skill than to allot them such a time-limit as this,” wrote the editors. “But certainly anyone who can solve this problem in three or four hours will have good cause to be congratulated on his ingenuity.”
When the Chevalier de Rohan was sent to the Bastille in 1674 on suspicion of treason, he knew there was no evidence against him except what might be extracted from one other prisoner. His friends had promised to communicate the result of that examination, and in sending him some fresh clothing they wrote on one of the shirts MG DULHXCCLGU GHJ YXUJ, LM CT ULGC ALJ.
For 24 hours de Rohan puzzled over the message, but he could make no sense of it. Despairing, he admitted his guilt and was executed. What was the message?

From Henry Dudeney:
The ilustration represents a square tablecloth of choice silk patchwork. This was put together by the members of a family as a little birthday present for one of its number. One of the contributors supplied a portion in the form of a perfectly symmetrical star, and this has been worked in exactly as it was received. But the triangular pieces so confuse the eye that it is quite a puzzle to find the hidden star.
Can you discover it, so that, if you wished, by merely picking out the stitches, you could extract it from the other portions of the patchwork?

Amy and Betty are playing a game. They have a chocolate bar that’s 8 squares long and 6 squares wide. Amy begins by breaking the bar in two along any division. Betty can then pick up any piece and break it in two, and so on. The first player who cannot move will be clapped in chains and rocketed off to a lifetime of soul-destroying toil in the cobalt mines of Yongar Zeta. (I know, it’s a pretty brutal game.) Who will win?
A logic puzzle from Mathematical Circles (Russian Experience), a collection of problems for Soviet high school math students:
During a trial in Wonderland the March Hare claimed that the cookies were stolen by the Mad Hatter. Then the Mad Hatter and the Dormouse gave testimonies which, for some reason, were not recorded. Later on in the trial it was found out that the cookies were stolen by only one of these three defendants, and, moreover, only the guilty one gave true testimony. Who stole the cookies?
A favorite problem of Lewis Carroll involves a customer trying to complete a purchase using pre-decimal currency. He wants to buy 7s. 3d. worth of goods, but he has only a half-sovereign (10s.), a florin (2s.), and a sixpence. The shopkeeper can’t give him change, as he himself has only a crown (5s.), a shilling, and a penny. As they’re puzzling over this a friend enters the shop with a double-florin (4s.), a half-crown (2s. 6d.), a fourpenny-bit, and a threepenny-bit. Can the three of them negotiate the transaction?
Happily, they can. They pool their money on the counter, and the shopkeeper takes the half-sovereign, the sixpence, the half-crown, and the fourpenny-bit; the customer takes the double-florin, the shilling, and threepenny-bit as change; and the friend takes the florin, the crown, and the penny.
“There are other combinations,” writes John Fisher in The Magic of Lewis Carroll, “but this is the most logistically pleasing, as it will be seen that not one of the three persons retains any one of his own coins.”
Related: From Henry Dudeney, a magic square:
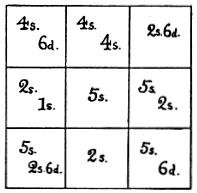
(Strand, December 1896)
A devilish puzzle by Lee Sallows:
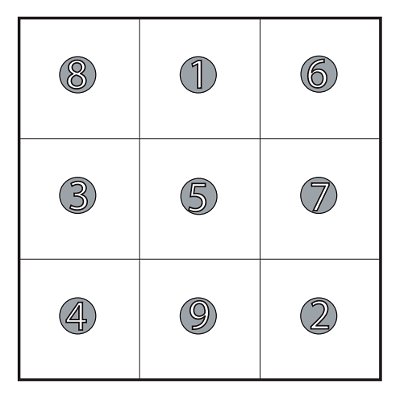
In the diagram above, nine numbered counters occupy the cells of a 3×3 checkerboard so as to form a magic square. Any 3 counters lying in a straight line add up to 15. There are 8 of these collinear triads.
Reposition the counters (again, one to each cell) to yield 8 new collinear triads, but now showing a common sum of 16 rather than 15.