Six boys are accused of stealing apples. Exactly two are guilty. Which two? When the boys are questioned, Harry names Charlie and George, James names Donald and Tom, Donald names Tom and Charlie, George names Harry and Charlie, and Charlie names Donald and James. Tom can’t be found. Four of the boys who were questioned named one guilty boy correctly and one incorrectly, and the fifth lied outright. Who stole the apples?
Puzzles
Playing With Food
A group of four missionaries are on one side of a river, and four cannibals are on the other side. The two groups would like to exchange places, but there’s only one rowboat, and it holds only three people, and only one missionary and one cannibal know how to row, and the cannibals will overpower the missionaries as soon as they outnumber them, either on land or in the boat. Can the crossing be accomplished?
Black and White
Sweet Reason
A brainteaser by Chris Maslanka:
A packet of sugar retails for 90 cents. Each packet includes a voucher, and nine vouchers can be redeemed for a free packet. What is the value of the contents of one packet? (Ignore the cost of the packaging.)
The Pill Scale (Part 2)
A variation on yesterday’s puzzle:
Suppose there are six bottles of pills, and more than one of them may contain defective pills that weigh 6 grams instead of 5. How can we identify the bad bottles with a single weighing?
The Pill Scale (Part 1)
An efficiency-minded pharmacist has just received a shipment of 10 bottles of pills when the manufacturer calls to say that there’s been an error — nine of the bottles contain pills that weigh 5 grams apiece, which is correct, but the pills in the remaining bottle weigh 6 grams apiece. The pharmacist could find the bad batch by simply weighing one pill from each bottle, but he hits on a way to accomplish this with a single weighing. What does he do?
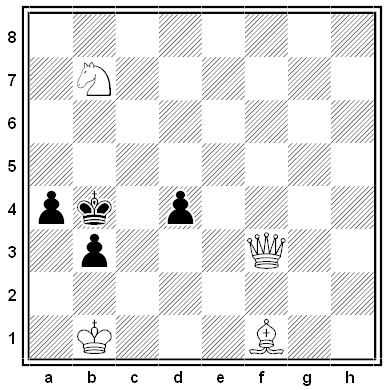
Black and White

This week’s puzzle has a twist: Imagine that the board has been rolled into a cylinder so that the a- and h-files are joined and pieces can move across the boundary. How can White mate in two moves?
Letters and Numbers
The first 10 letters of the alphabet, ABCDEFGHIJ, form a cipher that conceals the name of a number less than 100. What is the number?
Groaners
- How does a deaf man indicate to a hardware clerk that he wants to buy a saw?
- How can you aim your car north on a straight road, drive for a hundred yards, and find yourself a hundred yards south of where you started?
- What runs fore to aft on one side of a ship and aft to fore on the other?
- A very fast train travels from City A to City B in an hour and a quarter. But the return trip, made under identical conditions, requires 75 minutes. Why?
- Does Canada have a 4th of July?
- Exhausted, you go to bed at 8 p.m., but you don’t want to miss an appointment at 10 a.m. the next day, so you set your alarm clock for 9. How many hours do you sleep?