
Norwegian broadcaster NRK presented this problem during its coverage of the 2021 FIDE World Chess Championship in Dubai. White is to give mate on the move. (Warning — there’s a trick.)

Norwegian broadcaster NRK presented this problem during its coverage of the 2021 FIDE World Chess Championship in Dubai. White is to give mate on the move. (Warning — there’s a trick.)
A pleasing puzzle by Eric LeVasseur:
PI × R2 = AREA
If each letter in this expression (but not the exponent 2) is replaced with a corresponding digit, the resulting equation will be valid. What are the digits?
Alice and Bob are two infinitely intelligent logicians. Each has a number drawn on their forehead. Each can see the other’s number but not their own. Each knows that both numbers are positive integers. An observer tells them that the number 50 is either the sum or the product of the two numbers. Alice says to Bob, “I do not know my number,” and Bob replies, “I do not know my number either.” What is Alice’s number?

A Brooklyn bookseller distributed this card during the 1880 U.S. presidential race between James Garfield and Winfield Scott Hancock. What does it say?
Alexander Shapovalov suggested an unusual coin-weighing problem for the sixth international Kolmogorov math tournament in 2007:
A judge is presented with 80 coins that all look the same, knowing that there are either two or three fake coins among them. All the real coins weigh the same and all the fake coins weigh the same, but the fake coins are lighter than the real ones.
A lawyer knows that there are exactly three fake coins and which ones they are. The lawyer must use a balance scale to convince the judge that there are exactly three fake coins and that it is impossible for there to be only two fake coins. She is bound by her contract not to reveal any information about any particular coin. How should she proceed?
The lawyer might try dividing the 80 coins into three groups of 26, each group containing one fake coin, with two coins left over. With two weighings she could then show that the three groups have the same weight. From this the judge could conclude that either (a) there are 3 fake coins, one in each group, or (b) there are 2 fake coins, both in the leftover group. The lawyer could then weigh one of the leftover coins against a real coin taken from one of the three groups, to show that these balance. This would prove to the judge that there are 3 fake coins (because if there were only 2 then possibility (b) above would be ruled out). However, this strategy is “indiscreet” — it would reveal to the judge the true character of each of the leftover coins, which the lawyer has pledged not to do. How should she proceed instead?
I just stumbled into this — in October 1967, IBM published this problem in Eureka, the journal of the Cambridge University Mathematical Society (page 2):
The triplets (whose abilities at walking, cycling, and donkey riding are identical) always leave home together at the last possible minute and arrive at school together on the last stroke of the bell.
They used to walk the 4 1/2 miles, and so had to set out at 8.00; then they acquired a bicycle and found that they did not have to leave home until 8.15 (Charles rode it for the first 1 1/2 miles, left it, and walked on; Donald walked 1 1/2 miles, cycled 1 1/2 miles, and walked again; Edward walked 3 miles and cycled the rest). More recently they have been given a donkey. After experiments to determine the donkey’s speed and to verify that it stood stock still when left, they found that — using the bicycle and the donkey — they did not need to leave home until 8.25. There were several schemes of changing over which they could use to do this, of course; but naturally they chose a scheme which involved the minimum number of changes. Going to school tomorrow Charles will start on foot and Edward will arrive on foot. How far will Donald walk?
In place of an answer they listed the address of their London office, as an invitation to prospective systems analysts. I can’t see that they ever published a solution to the puzzle; I’m posting it here for what it’s worth.
07/01/2024 UPDATE: Reader Catalin Voinescu supplies the solution:
Riding the bicycle for 1.5 miles takes 15 fewer minutes than walking the same distance, so the bicycle saves 10 minutes per mile (compared to walking).
Another way to look at it is that riding the bicycle 4.5 miles saves three people 15 minutes, or an aggregate of 45 person-minutes (see ‘man-month’, another concept popular at IBM at the time; ‘The Mythical Man-Month’, an excellent book by Frederick P. Brooks, Jr, explores this in detail).
Riding the donkey 4.5 miles saves a total of 30 person-minutes, or 6 2/3 minutes per mile (compared to walking).
It’s not possible for any person not to change means of transportation, because they would arrive too late (walking) or too early (other means of transportation). For the same reason, it’s not possible for each person to change only once, because whoever got the bike and the donkey and did not walk at all would also arrive too early. Thus, the minimum number of changes is four, with one person walking and riding the donkey, another person walking and riding the bike (not necessarily in this order), and the third doing all three.
The person who walks and rides the bike needs to save 25 minutes, so they need to ride the bike for 2 1/2 miles and walk 2 miles. Assume they do it in this order (see below). The person who switches twice needs to ride the bike for the final 2 miles.
The person who walks and rides the donkey needs to save the same 25 minutes, which, at a rate of 6 2/3 minutes saved per mile, means 3 3/4 mile of riding the donkey and 3/4 mile of walking. They have to walk first and then ride the donkey, because the person who switches twice needs to ride the donkey for the remaining 3/4 mile, and they can only do this at the beginning (we already have them biking at the end).
The person who switches twice rides the donkey for 3/4 mile at the beginning, and bikes for 2 miles at the end. In between, they walk the remaining 1 3/4 mile.
So: Edward bikes 2 1/2 miles then walks 2 miles. Donald rides the donkey 3/4 mile, walks 1 3/4 mile, then rides the bike 2 miles. Charles walks 3/4 mile, then rides the donkey for the remaining 3 3/4 miles.
If we assume the person who walks and rides the bike does them in the opposite order, we get a mirrored solution: Edward rides the donkey for 3 3/4 miles and walks 3/4 mile; Donald rides the bike for 2 miles, walks 1 3/4 mile, then rides the donkey 3/4 mile; and Charles walks 2 miles, then picks up the bike and rides it for the remaining 2 1/2 miles.
In both cases, Donald walks 1 3/4 mile.
Other solutions exist, but they require more than four changes. It’s even possible for the three people to each walk, ride the donkey and bike equal distances (1 1/2 mile of each, each), but I don’t know what minimum number of changes that would require (more than six, and not all 1 1/2 mile stretches can be contiguous).
(Thanks, Catalin.)
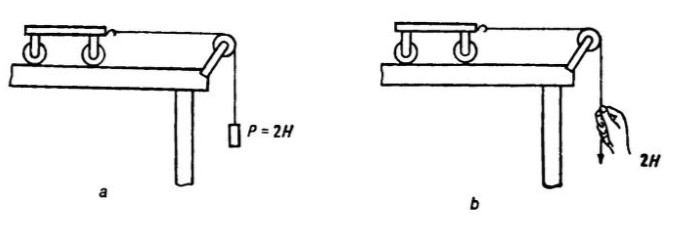
These two handcarts have the same mass. Newton tells us that equal forces applied to equal masses impart equal accelerations. So why does the second handcart pick up speed more quickly than the first? (This is a Soviet problem; Н is the Russian abbreviation for newtons.)
From reader Éric Angelini: During a standard chess game, after Black’s fifth move we notice that three rooks have been captured on the same dark square. Which square is it?
A conference is attended by 1,000 delegates from various countries. It’s known that any three delegates can speak together without help, though one of the three may have to serve as interpreter for the other two. Prove that all the attendees can be accommodated in double rooms so that the two occupants of each room can speak to each other.
D.C.B. Marsh proposed this problem in the American Mathematical Monthly in 1957:
“Solve a3 – b3 – c3 = 3abc, a2 = 2(b + c) simultaneously in positive integers.”
There are a number of ways to go about this, but Raymond Huck of Marietta College found a strikingly simple one. 3abc is positive, so the first equation tells us immediately that b < a and c < a. Add these two facts together and we get b + c < 2a, and hence 2(b + c) < 4a. Substituting this conveniently into the second equation, we learn that a2 < 4a and a < 4. The second equation also shows that a is an even number, so a must be 2, and b and c, which are smaller, must both be 1.
(“Solutions,” American Mathematical Monthly 65:1 [January 1958], 43-46, Problem E1266, via Ross Honsberger, Mathematical Morsels, 1979.)