Puzzles
Firelight
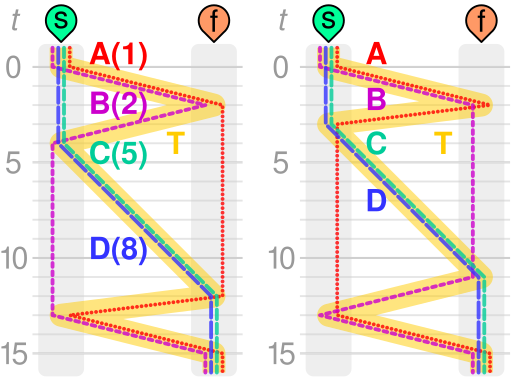
Four people are traveling in the dark when they arrive at a river. The narrow bridge can accommodate only two people at a time, and the group has only one torch, which must accompany each party that makes a crossing. Persons A, B, C, and D can cross in 1, 2, 5, and 8 minutes, respectively, and any pair of travelers can move only at the pace of the slower person. The torch will go out in 15 minutes. Can they all get safely across?
The Heist
A puzzle by Jared Z., Nicole H., and Benjamin E., mathematicians at the National Security Agency:
The chief detective hurried down to the police station after hearing big news: there was a heist at Pi National Bank! The police had brought in seven known gang members seen leaving the scene of the crime. They belonged to the nefarious True/False Gang, so named because each member is either required to always tell the truth or required to always lie, although everyone is capable of engaging in wrongdoing. The chief also knew from his past cases that any crime committed by the gang always included one truth teller.
When the chief showed up, he asked the gang members the following questions:
1) Are you guilty?
2) How many of the seven of you are guilty?
3) How many of the seven of you tell the truth?
Here were their responses:
Person 1: Yes; 1; 1
Person 2: Yes; 3; 3
Person 3: No; 2; 2
Person 4: No; 4; 1
Person 5: No; 3; 3
Person 6: No; 3; 3
Person 7: Yes; 2; 2
After looking these answers over, the chief prepared to arrest those responsible.
Which of these seven did the chief arrest?
Yajilin
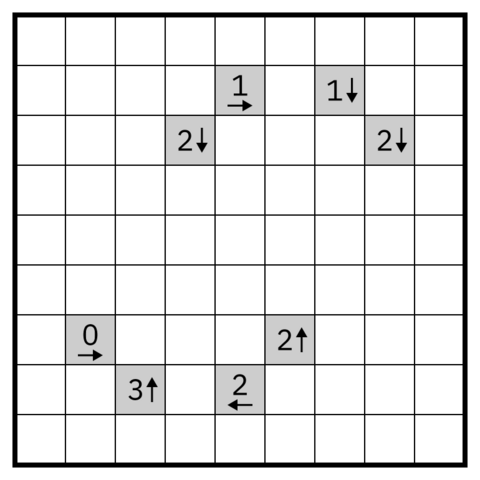
The goal of this logic puzzle is simple: to draw an orthogonally connected, non-intersecting loop that passes through every white square on the board. The trouble is that the board contains some number of black squares, and these are hidden. The only clues to their location are the numbers in the gray squares. In the diagram above, there are exactly 3 black squares in the third file north of the “3” indicator. And there are no black squares on the third rank anywhere east of the “0” indicator.
Gray squares can’t be black, no two black squares are orthogonally adjacent, and there may be some black squares that aren’t referred to by any of the indicators.
Knowing all this (and knowing that a solution is possible), can you determine the location of all the black squares and draw a loop that passes through all the white ones?
Black and White

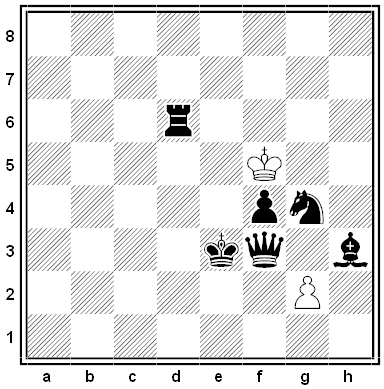
A logic problem in the shape of a chess puzzle, by Éric Angelini. White has just moved. What was his move?
In the Fold
Just found this on Wikimedia Commons — “Where Is the Fifth Pig?”, an anonymous puzzle created in occupied Holland in 1940:




A Little Clue
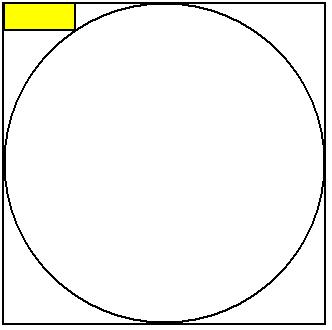
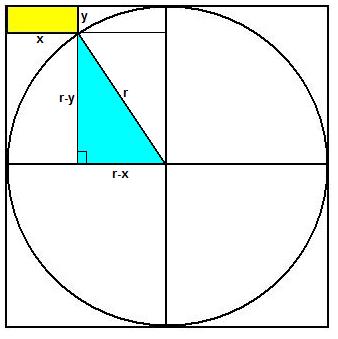
A circle is inscribed in a square, with a rectangle drawn from a corner of the square to a point on the circle, as shown. If this rectangle measures 6 inches by 12 inches, what’s the radius of the circle?
Also-Rans
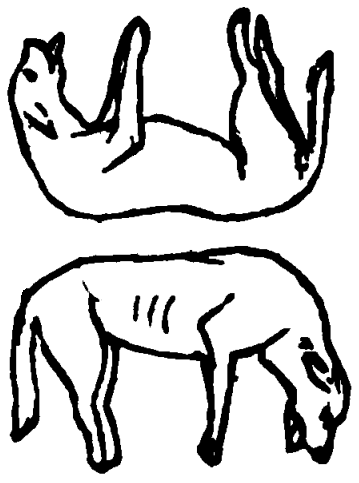
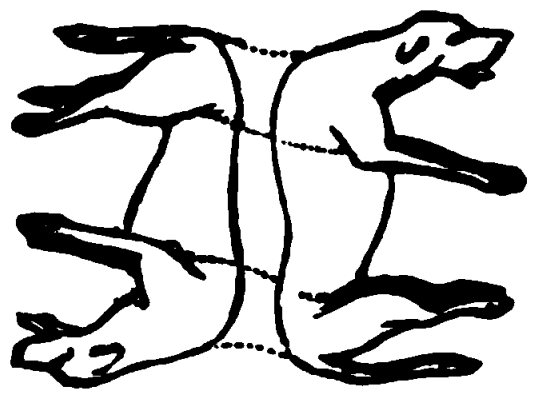
“The dogs are, by placing two lines upon them, to be suddenly aroused to life and made to run. Query, How and where should these lines be placed, and what should be the forms of them?”
Backward and Forward
John Grant McLoughlin offered this problem in Crux Mathematicorum in April 2008:
Every four-digit numerical palindrome (e.g., 2772) is a multiple of 11. Why is this?