These are the punts of Trinity College, Cambridge, moored on the River Cam. What is the significance of their names?
Shipshape
Puzzles
Freight
A problem from Cambridge mathematician J.E. Littlewood’s Miscellany (1953):
Is it possible to pack a cube with a finite number of smaller cubes, no two of which are the same size?
Oh
A puzzle by Lewis Carroll:
Dreaming of apples on a wall,
And dreaming often, dear,
I dreamed that, if I counted all,
How many would appear?
Self-Destruction
This chess problem, from Wolfgang Pauly’s 1912 Theory of Pawn Promotion, is a selfmate in two: How can White force Black to deliver checkmate within two moves, despite Black’s best effort to avoid doing so? White moves first.
Gun Control
Marksman A hits a certain small target 75 percent of the time. Marksman B hits it 25 percent of the time. The two of them aim at that target and fire simultaneously. One bullet hits it. What’s the probability that it came from A?
Branch Manager
A puzzle from The Book of the Thousand Nights and One Night:
“Solve the following problem if you can: a flock of pigeons alighted upon a tree, some perching upon the upper branches and some upon the lower; those upon the upper branches said to those upon the lower: ‘If one of you flies up to us our number will be double yours; if one of us flies down to you, our numbers will be equal.'”
How large was the flock?
A Syntax Maze
David Morice posed this puzzle in the February 1989 issue of Word Ways. The following sentence is such a thicket of interrupting clauses that it’s difficult to divine its meaning. Who is accused, what’s the verdict, what are the crimes, and what’s the real name of the real criminal? “Let’s see you unChandler this one!”
Big Mike, when Susan, without whom he, whose rugged jaw, as he muttered, “Why did you, who committed, after you changed your name, though nobody –” but he paused, while he glared at her, even though Melissa thought, which seemed immaterial, for the courtroom, where the judge, before the verdict, whether Big Mike was guilty, though Melissa, since Ted no longer, however she, when Big Mike, because she blamed him, while the cops, who trusted, although they sensed, until Detective Jennings, against his better judgment, fell in love with the lady, her guilt, her innocence, held him at gunpoint, for her bank robbery, was picked up, played her cards, wanted to buy diamonds for her, murdered him with a dagger, or framed, could be decided, heard Susan’s surprise testimony, was packed with an angry mob, to the prosecuting attorney, of Ted as her real lover, in the witness stand, to catch his breath, “– seems to realize, from Melissa to Joyce, both crimes, lay your rap on me?” under his breath, was clenched bitterly, wouldn’t have been arrested, fingered him, was found guilty!
The Diabolical Cube
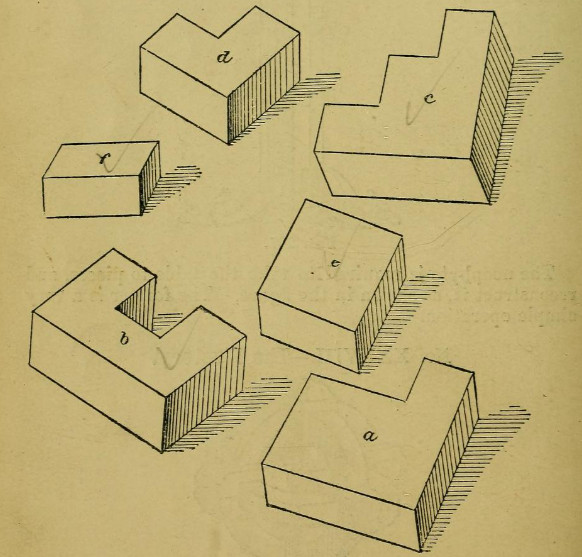
This is believed to be the oldest puzzle of its type, offered by Angelo Lewis in 1893.
“Of these six segments the experimenter is required to form a cube.”
The Three-Dice Problem
In 1620, the Grand Duke of Tuscany wrote to Galileo with a puzzling problem. In rolling three fair six-sided dice, it would seem that the sums 9 and 10 should appear with equal frequency, as there are six ways to produce each result:
10 = 6 + 3 + 1 = 6 + 2 + 2 = 5 + 4 + 1 = 5 + 3 + 2 = 4 + 4 + 2 = 4 + 3 + 3
9 = 6 + 2 + 1 = 5 + 3 + 1 = 5 + 2 + 2 = 4 + 4 + 1 = 4 + 3 + 2 = 3 + 3 + 3
But the duke had noticed that in practice 10 appears somewhat more often than 9. Why is this?
Galileo considered the problem and put his finger on the reason. What is it?
Checkless Chess
In checkless chess it’s illegal to give check without giving checkmate. This changes the whole complexion of the game. T.R. Dawson published this example in Die Welt in 1951. White is to mate in two moves.
The answer, 1. f6, threatens 2. Qf5, which strangely is mate because the black king can’t move off the long light diagonal, since that would discover check by the black bishop without giving checkmate. Black can try to prevent this finish by playing 1. … Qc8, guarding f5 and thus making 1. Qf5 itself illegal. But this permits 2. Nxd6, which now is mate because the black king has nowhere to run on the long diagonal and 2. … cxd6 is illegal because this would give a mateless check.
Similarly, if Black tries to stop 1. Qf5# with 1. … Qxf6, then 2. Nc5 is mate because Black can’t capture the knight — again, this would expose White’s king to an illegal check. And if Black tries to answer White’s first move with 1. … d5, to block the long light diagonal and free his king to flee elsewhere, then White can play 2. Qe5#, an ordinary (and legal) mate.