In a set of weights, no weight exceeds 10 kg. If the set is divided arbitrarily into two groups, the combined mass of one of these groups also will not exceed 10 kg. What’s the greatest possible mass of the full set of weights?
Puzzles
Endangered Species
Kevin Purbhoo invented this vivid puzzle while a student at Northern Secondary School in Toronto:
On a remote Norwegian mountain top, there is a huge checkerboard, 1000 squares wide and 1000 squares long, surrounded by steep cliffs to the north, south, east, and west. Each square is marked with an arrow pointing in one of the eight compass directions, so (with the possible exception of some squares on the edges) each square has an arrow pointing to one of its eight nearest neighbors. The arrows on squares sharing an edge differ by at most 45 degrees. A lemming is placed randomly on one of the squares, and it jumps from square to square following the arrows. Prove that the poor creature will eventually plunge from a cliff to its death.
Round Trip
An interesting query by Bob High, posed in the May-June 1994 issue of MIT Technology Review: Suppose a billiard ball with a small black dot precisely on its top is rolled around the full circumference of a circle of the same radius. Assuming no slippage or twisting, where is the dot when the ball returns to its starting point?
Black and White
Unorthodox Behavior
A puzzle from the 18th century — punctuate this sentence so that it makes sense:
King Charles the First walked and talked half an hour after his head was cut off.
Quickie
Punctuate this expression so that it makes sense:
Time flies you cannot they pass at such irregular intervals.
Going Up
A puzzle by Virginia McCarthy:
A 20-story office building has one busy elevator. On a recent trip upward, the elevator transported seven passengers. Each of these went up at least two floors, but no two of them went up the same number of floors. On this one upward journey, no more than one passenger crossed the elevator’s threshold on any given floor; no passenger exited on the 17th floor; and the elevator’s doors opened at more odd-numbered floors than even-numbered floors. Anton was the last passenger on and the second one off. Bessie got on before Clara and after Dagwood and went up more floors than Dagwood did. Edsel went up exactly twice as many floors as Filbert and got off before Gerda got on. Gerda was not the last one to exit.
Where did each passenger enter and exit the elevator?
The Banner of St. George

A “simple but pretty little puzzle” by Henry Dudeney: If this flag measures 4 feet by 3 feet and presents equal areas of red and white bunting, how wide are the cross’s arms?
Matching Sums
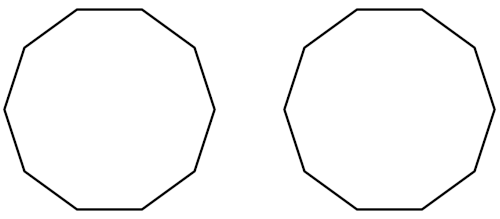
A puzzle by Russian mathematician Sergei Berlov:
Here are two decagons. Suppose that a positive integer is written at each of the 20 vertices such that the sum of the numbers around each decagon is 99. Prove that it’s possible to mark some number of successive vertices on each decagon so that the two sums of marked numbers are equal. (The marked segment on a given decagon may be a single vertex, but not all 10.)
Excerpts
J. Bryan III used to challenge his friends to think of an English word that contains either of the following strings of letters:
ILIL
ILIW
“I’ve never played the game with anyone who could solve either of these combinations.” Can you?

