Mr. Smith goes to Atlantic City to gamble for a weekend. To guard against bad luck, he sets a policy at the start: In every game he plays, he’ll bet exactly half the money he has at the time, and he’ll make all his bets at even odds, so he’ll have an equal chance of winning and of losing this amount. In the end he wins the same number of games that he loses. Does he break even?
Puzzles
Four Glasses
Martin Gardner published this puzzle in his “Mathematical Games” column in Scientific American in February 1979. You’re blindfolded and sitting before a lazy susan. On each corner is a glass. Some are right side up and some upside down. On each turn you can inspect any two glasses and, if you choose, reverse the orientation of either or both of them. After each turn the lazy susan will be rotated through a random angle. When all four glasses have the same orientation, a bell will sound. How can you reach this goal in a finite number of turns?
“Through the Looking-Glass”
C.S. Kipping published this unusual problem in Chess Amateur in 1923. In each position, White is to mate in two moves.
A Belt Font
Suppose you have a collection of gears pinned to a wall (disks in the plane). When is it possible to wrap a conveyor belt around them so that the belt touches every gear, is taut, and does not touch itself? This problem was first posed by Manuel Abellanas in 2001. When all the gears are the same size, it appears that it’s always possible to find a suitable path for the belt, but the question remains open.
Erik Demaine, Martin Demaine, and Belén Palop have designed a font to illustrate the problem — each letter is a collection of equal-sized gears around which exactly one conveyor-belt wrapping outlines an English letter:
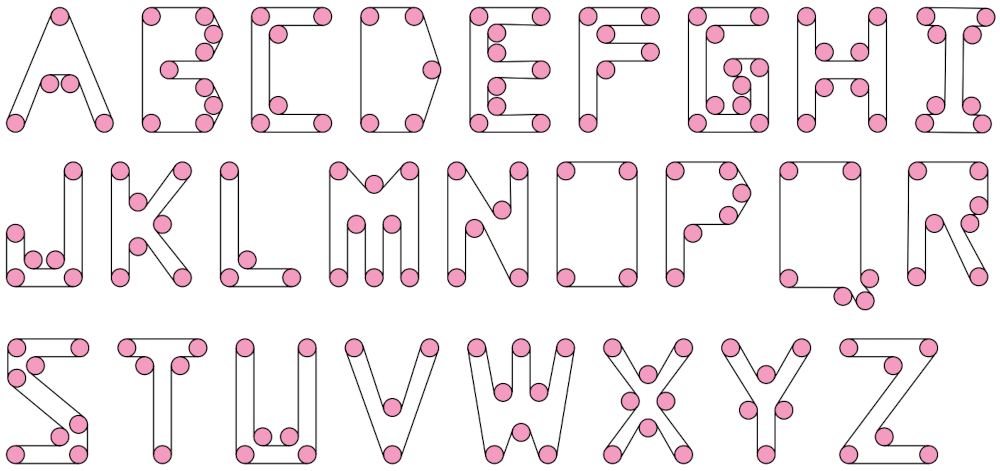
Apart from its mathematical interest, the font makes for intriguing puzzles — when the belts are removed, the letters are surprisingly hard to discern. What does this say?

The Desk Calendar

This is a variation on an old puzzle by Martin Gardner. This desk calendar currently displays the date Monday, April 25. If the six cubes are capable of displaying any day of the week and any date from January 01 to December 31, what characters appear on the unseen faces in the picture? Gardner wrote, “It is a bit trickier than one might expect.”
Sir Hilary’s Prayer

English poet Winthrop Mackworth Praed was renowned for his charades — this one, published in the 1830s, has never been solved:
Sir Hilary charged at Agincourt,–
Sooth, ’twas an awful day!
And though in that old age of sport
The rufflers of the camp and court
Had little time to pray,
’Tis said Sir Hilary mutter’d there
Two syllables by way of prayer.
My first to all the brave and proud
Who see to-morrow’s sun:
My next, with her cold and quiet cloud,
To those who find their dewy shroud
Before to-day’s be done:
And both together to all blue eyes,
That weep when a warrior nobly dies.
“The best answer I have been able to find is GOOD NIGHT,” wrote Henry Dudeney in 1919. “The two syllables are by way of wish or prayer. We wish nothing but good to the victorious, we leave those have fallen to their ‘dewy shroud’ at night, while to the sorrowful bereaved we cannot do less than wish them a good night.”
But Praed himself left no solution.
Black and White

“This seems to be my most ingenious two-mover,” wrote Vladimir Nabokov in 1970. He had composed it a year earlier in Montreux. White to mate in two moves.
Board Walk
Al writes the numbers 1, 2, …, 2n on a blackboard, where n is an odd positive integer. He then picks any two numbers a and b, erases them, and writes instead |a – b|. He keeps doing this until one number remains. Prove that this number is odd.
Floating Faster
A problem by Soviet physicist Viktor Lange:
It’s not uncommon to see two ships traveling down a river at different velocities — this is due to differences in design and engine power.
“But why can rafts which have no engines float down the river with different velocities, too? It has been even noticed that the heavier the raft the higher its velocity. Why is this?”
Nontransitive Tennis
A problem from the 17th Irish Mathematical Olympiad, in 2004:
In a tennis tournament, each player played one match against each of the others. If each player won at least one match, show that there’s a group of three players A, B, C in which A beat B, B beat C, and C beat A.