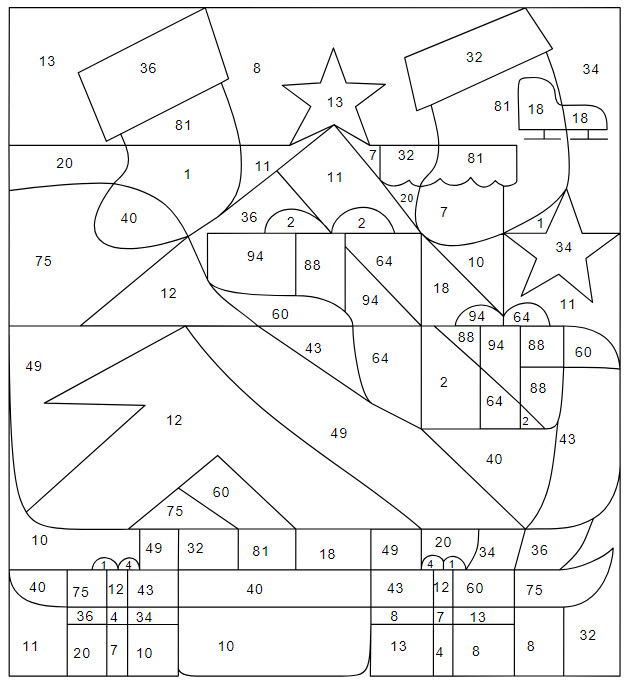
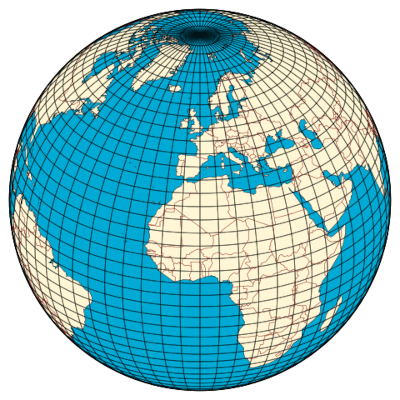
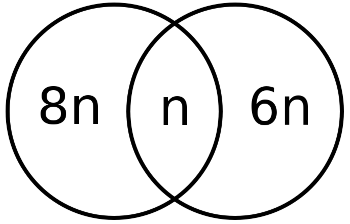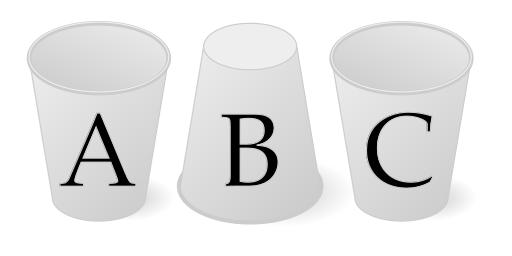The Royal Statistical Society’s Christmas Quiz runs through January 29 this year — 18 fiendish puzzles to mark the tradition’s 30th anniversary.
“Cracking the puzzles below will require a potent mix of general knowledge, logic, lateral thinking and searching skills — but, as usual, no specialist mathematical knowledge is needed.”
Entry is free and open to everyone. The top two entries will receive £100 and £50 in gift vouchers of their choice, and the quizmaster has pledged a donation of £900 to charities nominated by the top performers.
See the quiz web page for rules, entry instructions, and some tips for budding solvers.