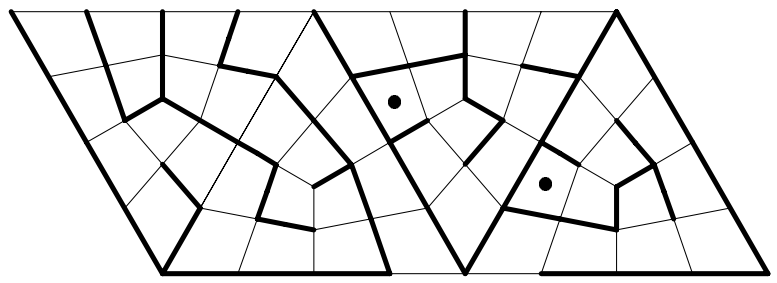
University of Ljubljana electrical engineer Izidor Hafner devised this maze on a tetrahedron, presented as an unfolded plane plan. Can you find a path from one dot to the other? To do so you’ll have to fold up the figure in your head:
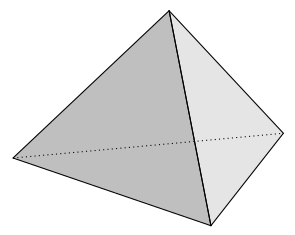

University of Ljubljana electrical engineer Izidor Hafner devised this maze on a tetrahedron, presented as an unfolded plane plan. Can you find a path from one dot to the other? To do so you’ll have to fold up the figure in your head:


By Augusto Piccinini. Imagine that the board is a vertical cylinder, that is, that the a-file and the h-file are joined so that pieces can move across the border. How can White mate Black in two moves?
You have 10 stacks of silver dollars, with 10 coins in each stack. The coins appear identical, but you know that all the coins in one stack are counterfeit. You know the weight of a genuine coin, and you know that a counterfeit coin weighs 1 gram less than this. How many weighings must you do to find the counterfeit stack?
An eight-digit number contains two 1s, two 2s, two 3s, and two 4s. The 1s are separated by 1 digit, the 2s by 2 digits, the 3s by 3 digits, and the 4s by 4 digits. What is the number?
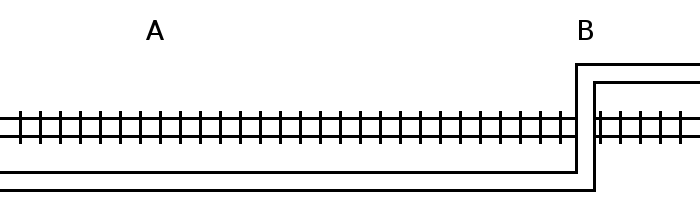
A problem from P.M.H. Kendall and G.M. Thomas’ Mathematical Puzzles for the Connoisseur, 1962: A road runs parallel to a railway until it bends to cross it, as shown. A man normally cycles to work along the road at a constant speed of 12 mph, and when he reaches the crossing he’s normally overtaken by a train traveling in the same direction. One day he was 25 minutes late for work and found that the train passed him 6 miles before the crossing. What was the speed of the train?
This question appeared in the 2015 Singapore and Asian Schools Math Olympiad, a competition for 14-year-old students from Singapore, Thailand, Vietnam, China, and the U.K. (I’ve amended the language a bit):
Albert and Bernard have just become friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates:
| May | 15 | 16 | 19 | |||
| June | 17 | 18 | ||||
| July | 14 | 16 | ||||
| August | 14 | 15 | 17 |
Cheryl then tells Albert and Bernard separately the month and the day of her birthday, respectively.
Albert: I don’t know when Cheryl’s birthday is, but I know that Bernard doesn’t know it either.
Bernard: At first I didn’t know when Cheryl’s birthday is, but I know now.
Albert: Then I also know when Cheryl’s birthday is.
When is Cheryl’s birthday?
Singapore TV presenter Kenneth Kong posted the question online, and it went viral in a matter of days. The competition organizers had intended it to “sift out the better students” and expected that 40 percent of the competitors would find the solution. What is it?