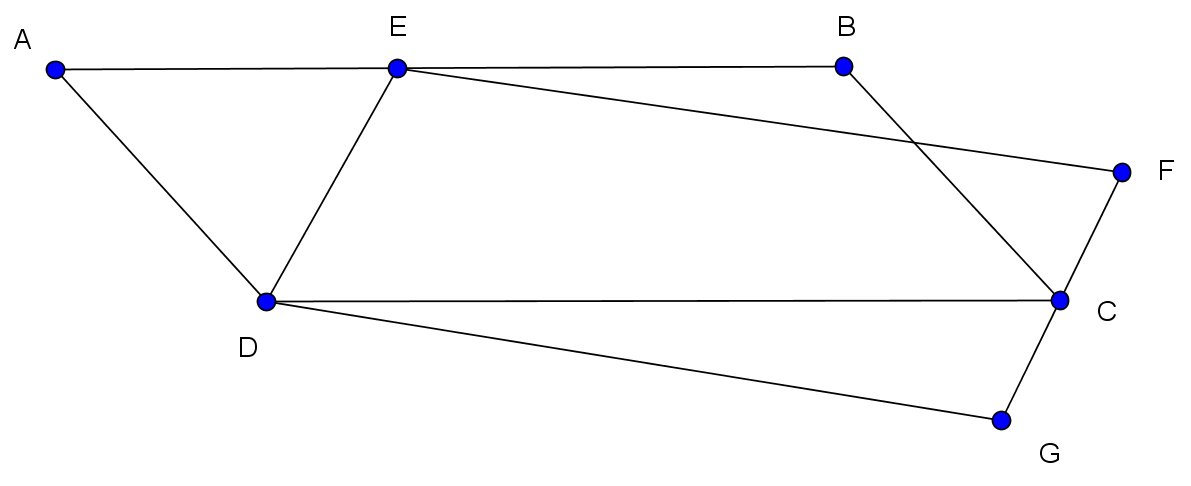
Parallelogram Puzzle

parallelogram puzzle

Point E lies on segment AB, and point C lies on segment FG. The area of parallelogram ABCD is 20 square units. What’s the area of parallelogram EFGD?

	Select Click for Answer
Draw EC. Now parallelogram ABCD and triangle EDC share a common base (DC), and they have the same altitude (a perpendicular from E to DC). So triangle EDC has half the area of parallelogram ABCD. But likewise, parallelogram EFGD and triangle EDC share a common base (ED), and they have the same altitude (a perpendicular from C to ED). So triangle EDC has half the area of parallelogram EFGD. Since both parallelograms have twice the area of the same triangle, their own areas must be equal. So the area of EFGD is 20 square units. (From Alfred S. Posamentier, Math Wonders to Inspire Teachers and Students, 2003.)

Click for Answer

August 10, 2016August 21, 2016 | Puzzles

Black and White

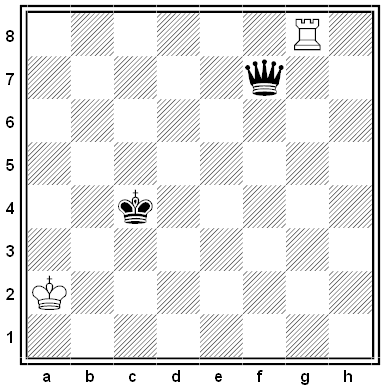
dawson chess puzzle

A “maximummer-selfmate” by T.R. Dawson, from 1934. White wants to force Black to checkmate him, and Black always makes the geometrically longest move available to him. How can White accomplish his goal in three moves?

	Select Click for Answer
1. Rb8 Qf1 2. Rb1 Qf8 3. Ka1 Qa3#. The distance from f8 to a3 $\left ( 5\sqrt{2} \approx 7.071 \right )$ is slightly greater than that from f8 to f1 (7 units).

August 5, 2016August 14, 2016 | Puzzles

All Roads

Another puzzle from Kendall and Thomas’ Mathematical Puzzles for the Connoisseur (1971):

Take three consecutive positive integers and cube them. Add up the digits in each of the three results, and add again until you’ve reached a single digit for each of the three numbers. For example:

46³ = 97336; 9 + 7 + 3 + 3 + 6 = 28; 2 + 8 = 10; 1 + 0 = 1
47³ = 103823; 1 + 0 + 3 + 8 + 2 + 3 = 17; 1 + 7 = 8
48³ = 110592; 1 + 1 + 0 + 5 + 9 + 2 = 18; 1 + 8 = 9

Putting the three digits in ascending order will always give the result 189. Why?

	Select Click for Answer
This repeated process of summing a number’s digits produces its digital root. One of the properties of digital roots is that when two numbers are multiplied, the digital root of the product is the same as the product of the digital roots of the two numbers themselves. Every positive integer has a digital root of from 1 to 9, and in the case of cubes: 1³ gives a digital root of 1 2³ gives a digital root of 8 3³ gives a digital root of 9 4³ gives a digital root of 1 5³ gives a digital root of 8 6³ gives a digital root of 9 And so on. As a result, the cubes of any three positive integers will always produce the digital roots 1, 8, 9 (in some order). UPDATE: Reader Hector Pefo offers a fuller explanation: Any sequence of three positive integers will include numbers that are 0, 1, and 2 mod 3 (that is, a multiple of 3, a number that is one more than a multiple of 3, and a number that is two more than a multiple of 3). The cube of a number that is 0 mod 3 is itself 0 mod 9, that of a number that is 1 mod 3 is 1 mod 9 (as can be seen by expanding the cube of 3n+1), and that of a number that is 2 mod 3 is 8 mod 9. Digital summation preserves a number’s value mod 9. For example, 3996 is 0 mod 9 and 4004 is 8 mod 9. The digital sum of 4004 comes from that of 3996 by subtracting 2 (final digit), adding 1 (first digit) and subtracting 18 (middle digits) for an overall effect of subtracting 19, which, mod 9, is the same as adding 8. And so the digital roots of numbers that are 0, 1, and 2 mod 3 will always be 9, 1, and 8.

Click for Answer

August 4, 2016August 14, 2016 | Puzzles

Perimeter Check

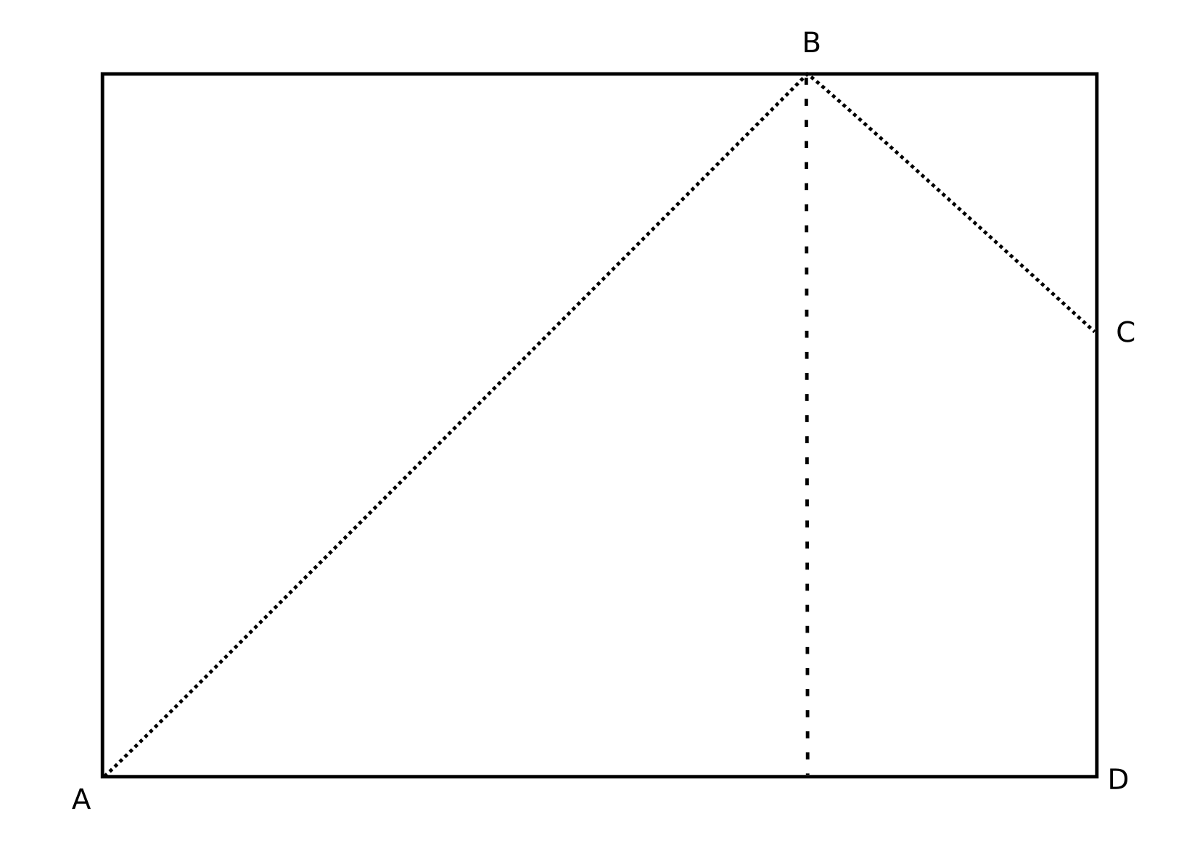
perimeter puzzle

A puzzle by Matt Parker of standupmaths:

The standard paper size A4 has dimensions in the ratio $1:\sqrt{2}$ . Hold a piece of A4 paper horizontally, as shown, and fold down the top left corner to meet the other side, creating fold AB, as if you were going to make a paper square. Then fold down the top right corner to meet the edge of this 1 × 1 square (making fold BC).

The perimeter of the original sheet was $\left ( 2 \times \sqrt{2} \right ) + \left ( 2 \times 1 \right )$ . What is the perimeter of the folded shape (the quadrilateral ABCD above)?

I’ll honor Matt’s request not to reveal the answer, but here’s a clue: The shape ABCD is a kite. See Matt’s video for a more visual explanation and a non-spoilery way to tell whether you have the right answer.

(Thanks to Dave Lawrence for the tip and the diagram.)

August 1, 2016July 31, 2016 | Puzzles

Mixing Day

A puzzle from P.M.H. Kendall and G.M. Thomas’ Mathematical Puzzles for the Connoisseur (1962):

Start with two containers, one holding green paint and the other an equal quantity of red paint.

Pour one pint of green paint into the red.
Pour two pints of this mixture back into the green.
Pour half the mixture in the green paint pot into the red pot.

Assume the paints are mixed thoroughly after each operation. If the two containers are now leveled off, without pouring any paint away, so that they both contain an equal quantity of paint, which pot is now more pure, the “green” paint or the “red”?

	Select Click for Answer
They’re equally pure. This is a fun puzzle because you can put the solver through any ludicrous number of operations and the answer is always the same. If we start and end with the same total quantity of paint in each pot, then any paint lost from the first pot must be replaced with paint from the second, and vice versa.

July 29, 2016August 7, 2016 | Puzzles

Five by Five

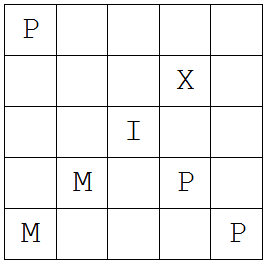
knuth latin square puzzle

Computer science legend Donald Knuth offered this puzzle at the 29th International Puzzle Party in San Francisco in August 2009. It’s a partially completed Latin square: The challenge is to place letters in the remaining cells so that each row and column contains the same five letters and in the bottom row these spell a common English word. The solution is unique.

	Select Click for Answer
Two further (harder) Latin square puzzles by Knuth are here. Solutions are here. (Donald Knuth, “Latin Square Word Puzzles,” Word Ways 42:4 [November 2009], 248.)

July 27, 2016August 7, 2016 | Puzzles

Black and White

meyer chess problem

By Heinrich Friedrich Ludwig Meyer. White to mate in two moves.

	Select Click for Answer
1. Bc8! half-pins both black rooks. Now Black has his choice of 23 different rook moves, but each of them allows the white knight to hop into either f4 or g5, giving mate. From the Boy’s Own Paper, 1908.

July 18, 2016July 24, 2016 | Puzzles

Road Work

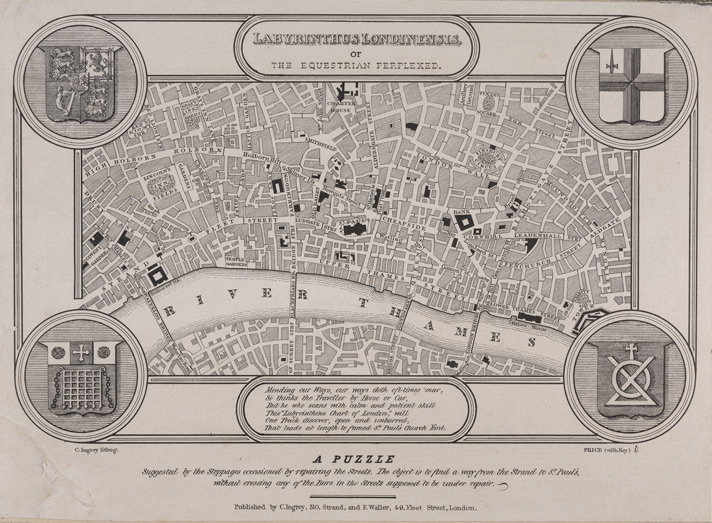
Fed up with endless traffic detours in 1830, London printer Charles Ingrey published a pointed puzzle, Labyrinthus Londoninensis, or The Equestrian Perplexed.

“The object is to find a way from the Strand [lower left] to St. Paul’s [center], without crossing any of the Bars in the Streets supposed to be under repair.”

Mending our Ways, our ways doth oft-times mar,
So thinks the Traveller by Horse or Car,
But he who scans with calm and patient skill
This ‘Labyrinthine Chart of London’, will
One Track discover, open and unbarred,
That leads at length to famed St. Pauls Church Yard.

The image above is a bit too small to navigate, but the British Library has an interactive zoomable version (requires Flash).

I don’t have the solution, but The Court Journal of Dec. 14, 1833, hints that “the farthest way round is the nearest way home.”

07/06/2022 UPDATE: A solution! (Thanks, Paul.)

July 16, 2016July 7, 2022 | Puzzles

Footwork

A poser from Penn State mathematician Mark Levi’s Why Cats Land on Their Feet (2012):

Using only a stopwatch and a sneaker, how can you find an approximate value for $\sqrt{2}$ ?

	Select Click for Answer
Suspend the sneaker by its lace to make a pendulum. Using the stopwatch, record the number of swings it makes in one minute, and call this n₁. Double the lace to halve its length and again record the number of swings in one minute. Call this n₂. Now $\sqrt{2}\approx n_{2}/n_{1}.$ For better precision, record the number of swings over a longer period of time. To estimate $\sqrt{3}$ , use a lace 1/3 as long, and so on.

Click for Answer

July 15, 2016July 24, 2016 | Puzzles

Hat Check

A puzzle from MIT Technology Review, July/August 2008:

Each of three logicians, A, B, and C, wears a hat that displays a positive integer. The number on one of the hats is the sum of the numbers on the other two. They make the following statements:

A: “I don’t know my number.”

B: “My number is 15.”

What numbers appear on hats A and C?

	Select Click for Answer
A is 10 and C is 5. The situation above, in which A doesn’t know his own number but B knows his after learning this, occurs if and only if (1) A and C have the same number or (2) A = 2C and B = 3C. Here’s the proof. If A and C have the same number, x, then B’s number must be 2x. Knowing this, A can conclude only that his own number must be either x or 3x, so he’ll declare that he doesn’t know his own number. B will see that both A and C bear the number x and declare that his own number is 2x. That takes care of (1). For (2), suppose that C’s number is x, A’s number is 2x, and B’s number is 3x. A can conclude only that his own number is either 2x or 4x, so he declares that he doesn’t know his own number. B can see that his own number must be x or 3x, but he realizes that he can eliminate x since, if that were the case, A would have seen two x‘s and could have concluded that his own number was 2x. So that shows that in cases (1) and (2) A and B will make the declarations presented in the puzzle statement. Now we have to show that these are the only cases that produce these two responses. So consider the three possibilities where A, then C, then B is the sum of the other two. (i) Here suppose C’s number is x, A’s is x + y, and B’s is y. If y = x, then A will see this and can conclude that his own number is 2x. If y ≠ x then A can’t know his own number. B knows that his own number must be either y or 2x + y. Neither of these numbers equals x, so both possibilities are consistent with A’s response, and B can’t know his number. (ii) Suppose C’s number is x + y, A’s is x, and B’s is y. A can’t tell whether his own number is x or x + 2y and so responds negatively. B knows that his number is either y or 2x + y. Neither number equals x + y, so B can’t eliminate either possibility and can’t know his own number. (iii) Here C’s number is x, A’s is y, B’s is x + y, and we know that x ≠ y (the case where x = y is covered under (1) above). So there are two possibilities: — If x > y then A responds negatively and B concludes that his own number must be either x + x or x – y. Neither of these possibilities equals x, so B can’t eliminate either one. — If x < y then A responds negatively and B concludes that his own number must be either x + y or y – x. Since x + y ≠ x, he can’t eliminate x + y. But he can eliminate y – x when y – x = x; that is, when y = 2x. This is (2) above, proving the claim. In this particular case we know that (1) is impossible since B claimed the number 15, an odd number. So (2) must be the case, and 3x = 15.

Click for Answer

A is 10 and C is 5. The situation above, in which A doesn’t know his own number but B knows his after learning this, occurs if and only if (1) A and C have the same number or (2) A = 2C and B = 3C.

Here’s the proof. If A and C have the same number, x, then B’s number must be 2x. Knowing this, A can conclude only that his own number must be either x or 3x, so he’ll declare that he doesn’t know his own number. B will see that both A and C bear the number x and declare that his own number is 2x.

That takes care of (1). For (2), suppose that C’s number is x, A’s number is 2x, and B’s number is 3x. A can conclude only that his own number is either 2x or 4x, so he declares that he doesn’t know his own number. B can see that his own number must be x or 3x, but he realizes that he can eliminate x since, if that were the case, A would have seen two x‘s and could have concluded that his own number was 2x.

So that shows that in cases (1) and (2) A and B will make the declarations presented in the puzzle statement. Now we have to show that these are the only cases that produce these two responses. So consider the three possibilities where A, then C, then B is the sum of the other two.

(i) Here suppose C’s number is x, A’s is x + y, and B’s is y. If y = x, then A will see this and can conclude that his own number is 2x. If y ≠ x then A can’t know his own number. B knows that his own number must be either y or 2x + y. Neither of these numbers equals x, so both possibilities are consistent with A’s response, and B can’t know his number.

(ii) Suppose C’s number is x + y, A’s is x, and B’s is y. A can’t tell whether his own number is x or x + 2y and so responds negatively. B knows that his number is either y or 2x + y. Neither number equals x + y, so B can’t eliminate either possibility and can’t know his own number.

(iii) Here C’s number is x, A’s is y, B’s is x + y, and we know that x ≠ y (the case where x = y is covered under (1) above). So there are two possibilities:

— If x > y then A responds negatively and B concludes that his own number must be either x + x or x – y. Neither of these possibilities equals x, so B can’t eliminate either one.

— If x < y then A responds negatively and B concludes that his own number must be either x + y or y – x. Since x + y ≠ x, he can’t eliminate x + y. But he can eliminate y – x when y – x = x; that is, when y = 2x. This is (2) above, proving the claim.

In this particular case we know that (1) is impossible since B claimed the number 15, an odd number. So (2) must be the case, and 3x = 15.

July 13, 2016July 24, 2016 | Puzzles