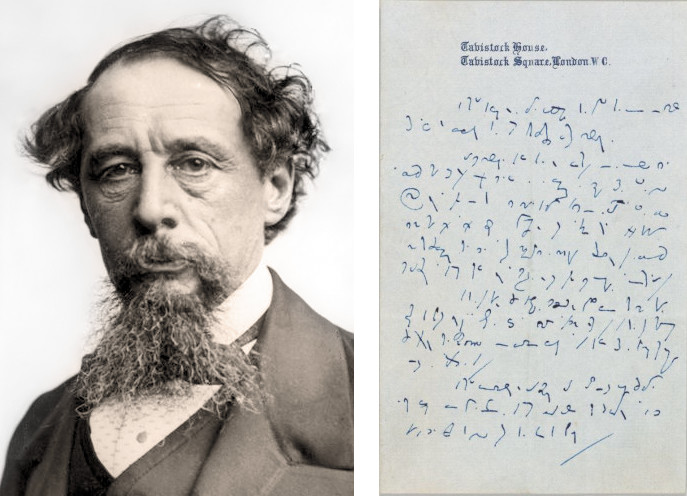What does this mean?
PMVEB DWXZA XKKHQ RNFMJ VATAD YRJON FGRKD TSVWF TCRWC
RLKRW ZCNBC FCONW FNOEZ QLEJB HUVLY OPFIN ZMHWC RZULG
BGXLA GLZCZ GWXAH RITNW ZCQYR KFWVL CYGZE NQRNI JFEPS
RWCZV TIZAQ LVEYI QVZMO RWQHL CBWZL HBPEF PROVE ZFWGZ
RWLJG RANKZ ECVAW TRLBW URVSP KXWFR DOHAR RSRJJ NFJRT
AXIJU RCRCP EVPGR ORAXA EFIQV QNIRV CNMTE LKHDC RXISG
RGNLE RAFXO VBOBU CUXGT UEVBR ZSZSO RZIHE FVWCN OBPED
ZGRAN IFIZD MFZEZ OVCJS DPRJH HVCRG IPCIF WHUKB NHKTV
IVONS TNADX UNQDY PERRB PNSOR ZCLRE MLZKR YZNMN PJMQB
RMJZL IKEFV CDRRN RHENC TKAXZ ESKDR GZCXD SQFGD CXSTE
ZCZNI GFHGN ESUNR LYKDA AVAVX QYVEQ FMWET ZODJY RMLZJ
QOBQ-
No one knows. Cryptologist Louis Kruh discovered it in the New York Public Library’s rare book room in 1993 among some old material from the U.S. Army Signal School. In 1915 first lieutenant Joseph O. Mauborgne had created what he believed was a more secure cipher than the ones currently in use, and had offered this challenge to see if his colleagues could break it. Kruh found no solution in the archive, and he published it in both The Cryptogram and Cryptologia, inviting their readers to try their hands at it. As far as I know, none succeeded.
Mauborgne described it as a “a simple, single-letter substitution cipher adapted to military use.” He invited the director of the Army Signal School to place it on a bulletin board and allow the officers there to work on it for three months and then to post the solution “to show why the standard method of attacking a substitution cipher fails in this case.” “If any attack upon this cipher is successful, I shall be glad to hear of it,” he wrote.
Kruh, who died in 2010, noted that “it was probably solved or otherwise deemed unsuitable for use because there is no knowledge of a new cipher being adopted by the Army around that time.” If a solution was found, I don’t believe anyone alive today knows what it is.
(Louis Kruh, “A 77-Year-Old Challenge Cipher,” Cryptologia 17:2 [April 1993], 172-174.)