“Some years ago there was a craze for rolling pellet puzzles,” wrote Henry Dudeney in 1909, “though they are really more trials of patience than puzzles.”
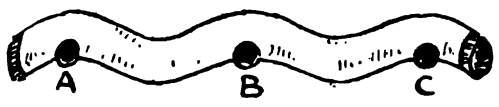
One exception was this undulated glass tube, which contained three shots or pellets. The task was to get them into the three depressions at A, B, and C, which are unfortunately positioned at high points in the tube.
This “could be solved by a puzzle trick which I was surprised to notice how few people discovered,” Dudeney wrote. What was it?
|
SelectClick for Answer |
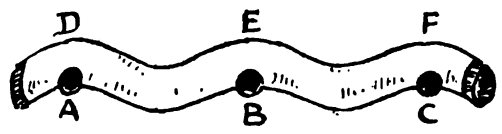
“The trick was to first reverse the tube so that the three depressions, D, E, and F, were at the bottom. It was quite easy to get the shots into these hollows, and when you had them in position you had merely to twist the tube with a quick turn of the fingers, holding it at the ends, when the pellets would fall into the required positions. You could hardly fail once in a hundred attempts, yet I have seen people try the puzzle for hours without success, while this simple trick never occurred to them.”
(Henry E. Dudeney, “The World’s Best Puzzles,” Strand 36:216 [January 1909], 692-700.)
|