Back in 2007 I noted the report of a curious wager in Berkshire in 1811: Sir John Throckmorton of Newbury bet a thousand guineas that he could have a coat made between sunrise and sunset of a single summer’s day, from the shearing of the sheep to the finished coat’s delivery by the tailor.

This appears to be true — in 1899 the Strand published a retrospective of the feat, including the first photo of the finished coat and the remarks of 93-year-old Charles Coxeter, the sole surviving witness and the younger brother of John Coxeter, the cloth manufacturer who had superintended most of the work. The sheep had been sheared at 5 a.m., and by 6:20 p.m. Throckmorton was able to don the finish coat before a crowd of 5,000 people, an hour and three-quarters before the deadline.

Coxeter was a curiously ambitious man: After the Battle of Waterloo he sponsored the preparation of a plum pudding 20 feet long, “which was cooked under the supervision of twelve ladies.” The “monster pudding” was carried to his house on a timber wagon drawn by two oxen and declared by all who partook “as nice as mother makes ’em.”

For his article “A Universal Money Pump for the Myopic, Naive, and Minimally Sophisticated,” in the April 2025 issue of Mind, philosopher Johan Gustafsson devised this minimal paradoxical stairway to illustrate a cyclic ranking: A appears higher than B, B appears higher than C, and C appears higher than A.

Two other perplexities, while we’re at it — by Mike Tolleb:

And by Wikimedia user Mabit1:

(Thanks, Johan.)

Socrates wants to cross a river and comes to a bridge guarded by Plato. The two speak as follows:

Plato: ‘Socrates, if in the first proposition which you utter, you speak the truth, I will permit you to cross. But surely, if you speak falsely, I shall throw you into the water.’

Socrates: ‘You will throw me into the water.’

Jean Buridan posed this conundrum in his Sophismata in the 14th century. Like a similar paradox in Don Quixote, it seems to leave the guardian in an impossible position — whether Socrates speaks truly or falsely, it would seem, the promise cannot be fulfilled.

Some readers offered a wry solution: Wait until he’s crossed the bridge, and then throw him in.

Another blue plaque, this one in Long Itchington, October 2014:

Related: Riverside, Iowa, is already congratulating itself as the future birthplace of James T. Kirk.

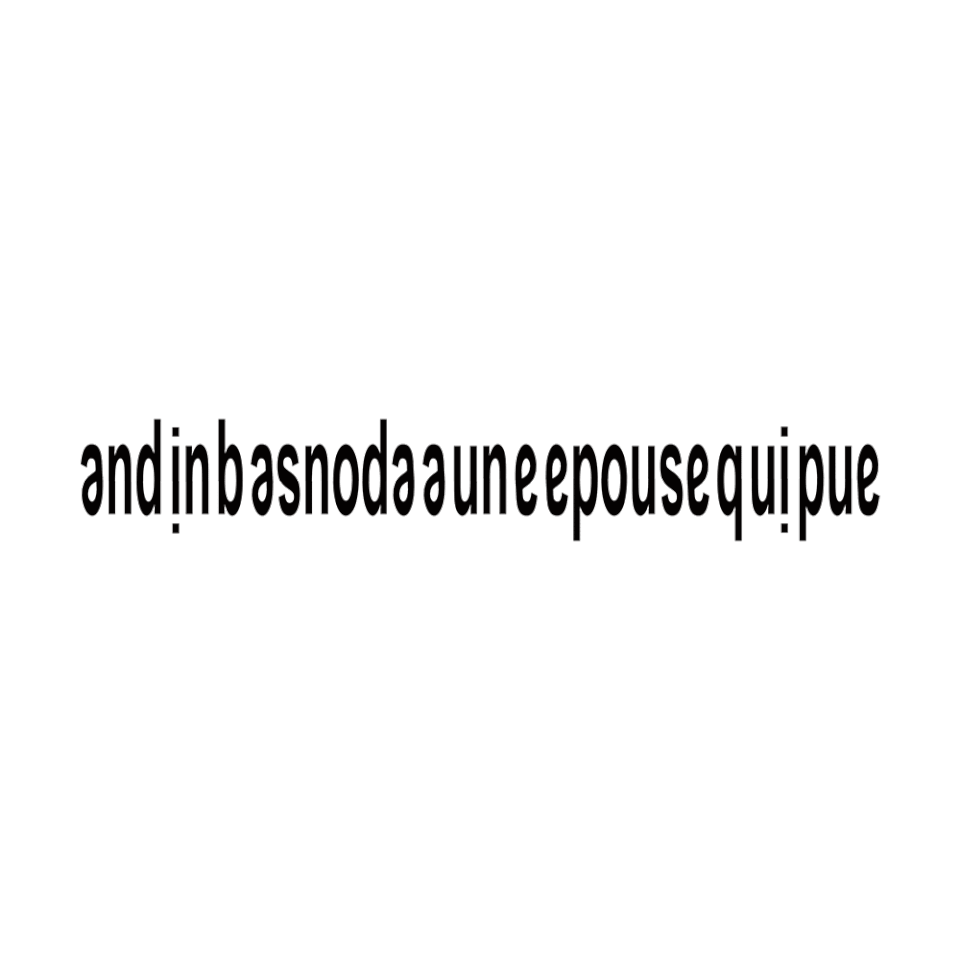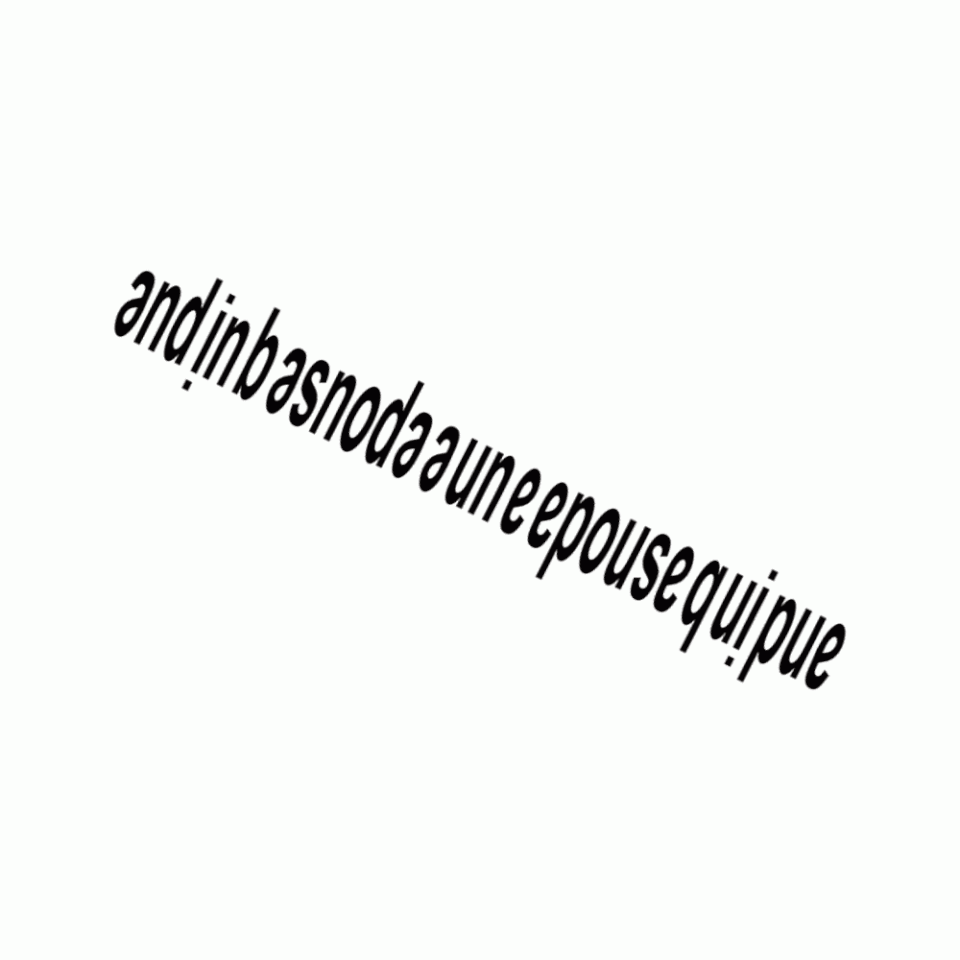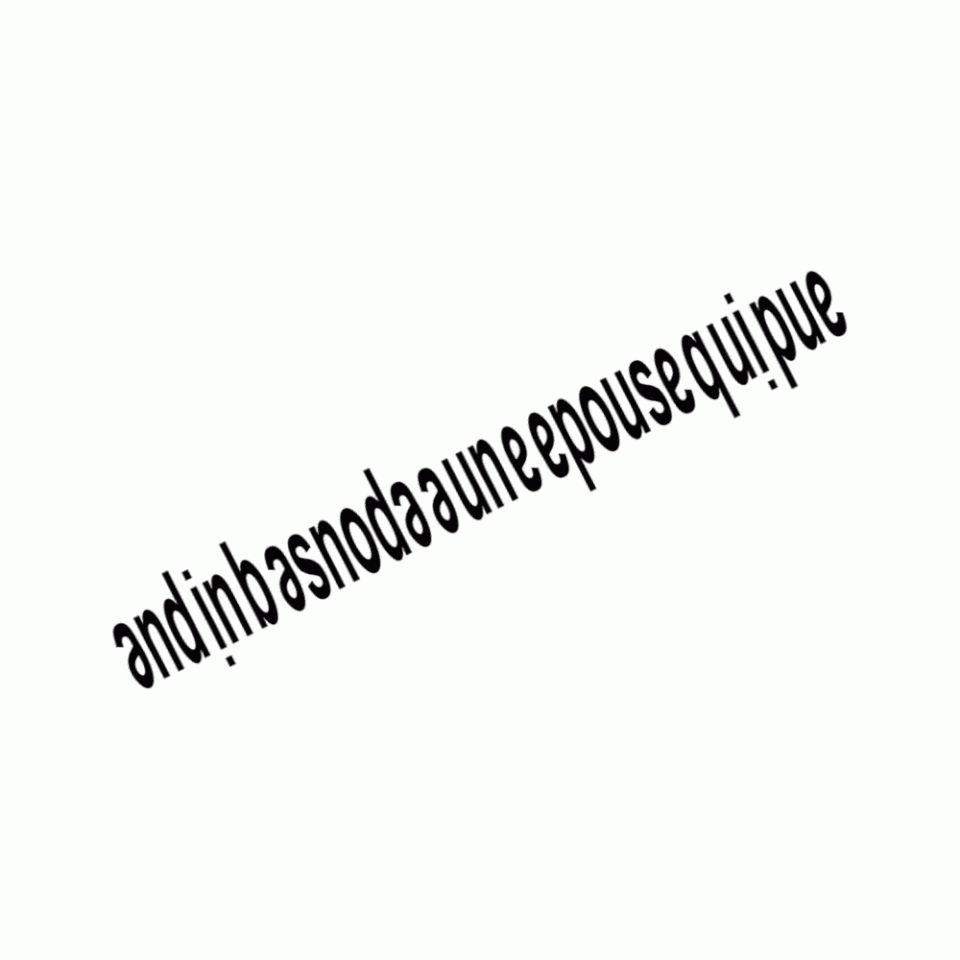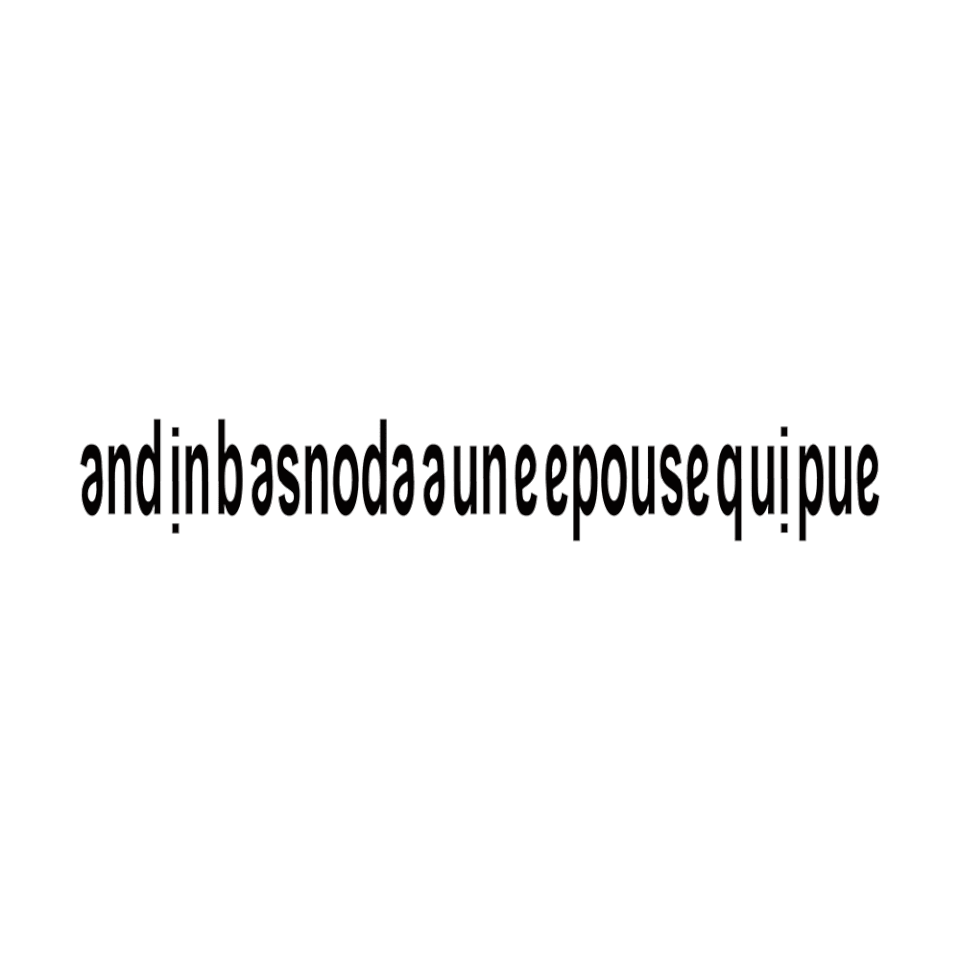
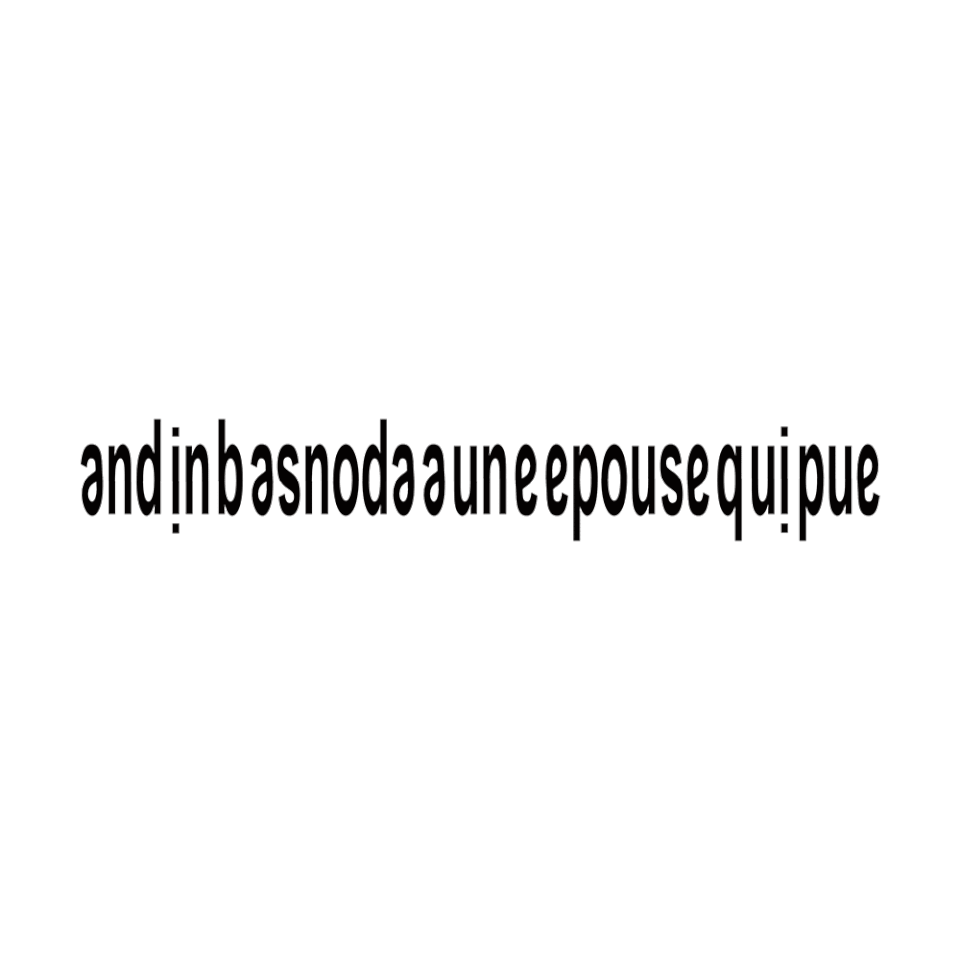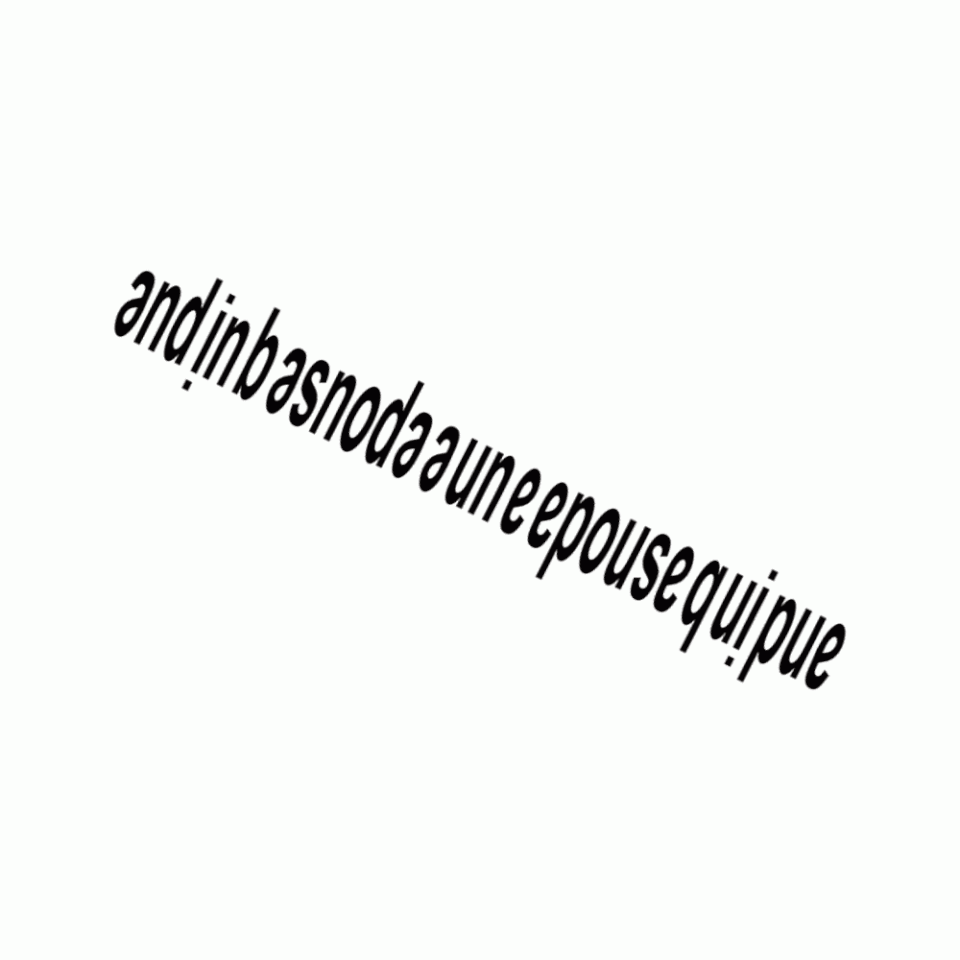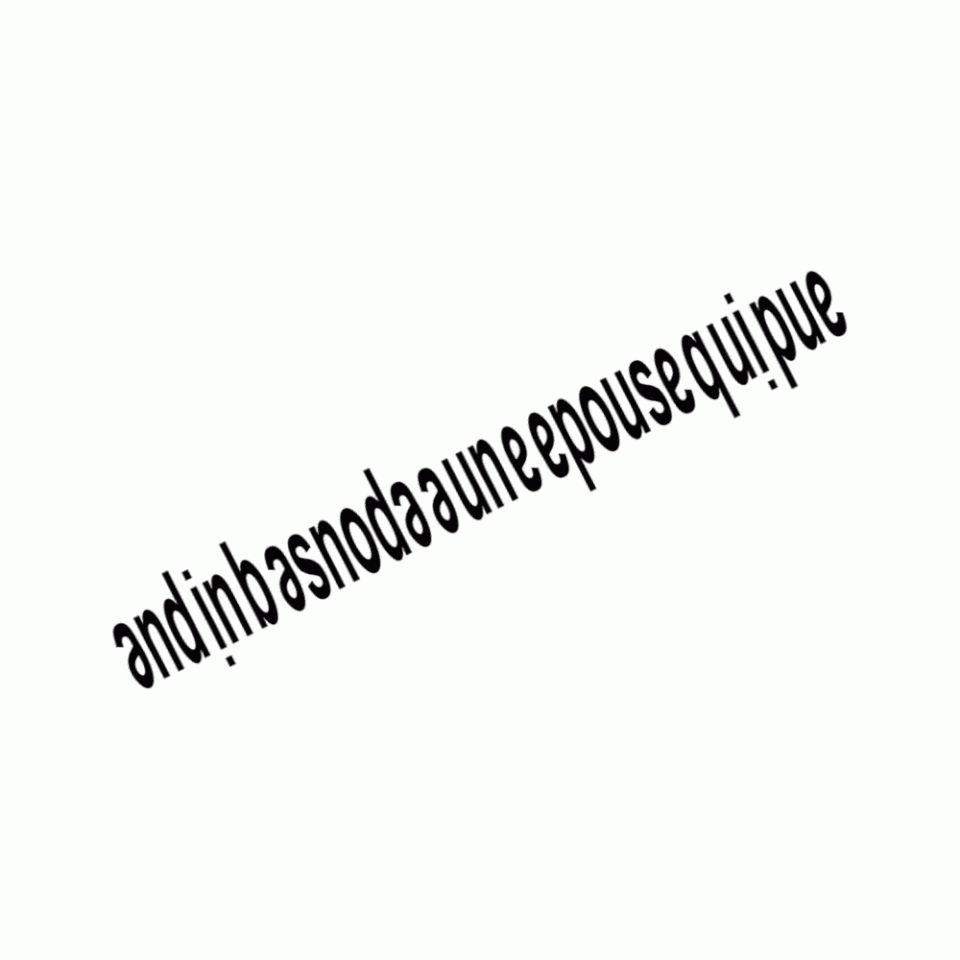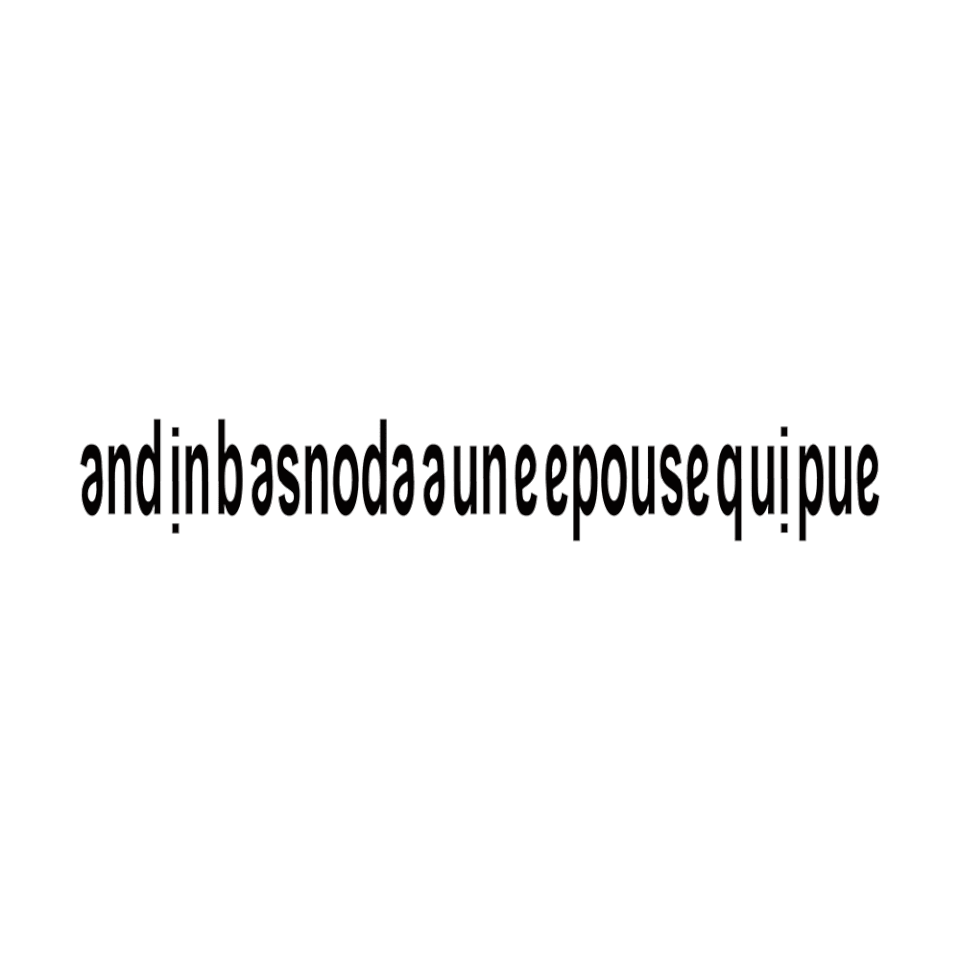
Georges Perec worked out that the French phrase andin basnoda a une epouse qui pue (“Andin Basnoda has a smelly wife”) reads the same upside down.

Typographer Pierre di Sciullo created a typeface to honor this ambigram — he called it Basnoda.

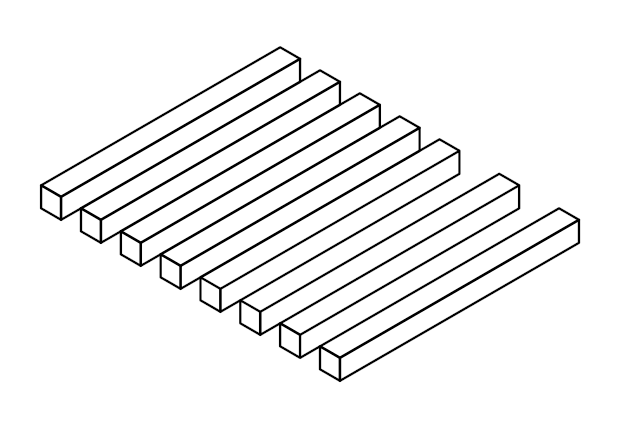
By Nevit Dilmen. How many sticks do you see?

Drive east along the shore of Lake Erie toward the town of Port Colborne, Ontario, and the mill before you appears to shrink, rather than grow, as you approach.

Similar: The Rowes Wharf Arch Anomaly:

See The Vista Paradox.