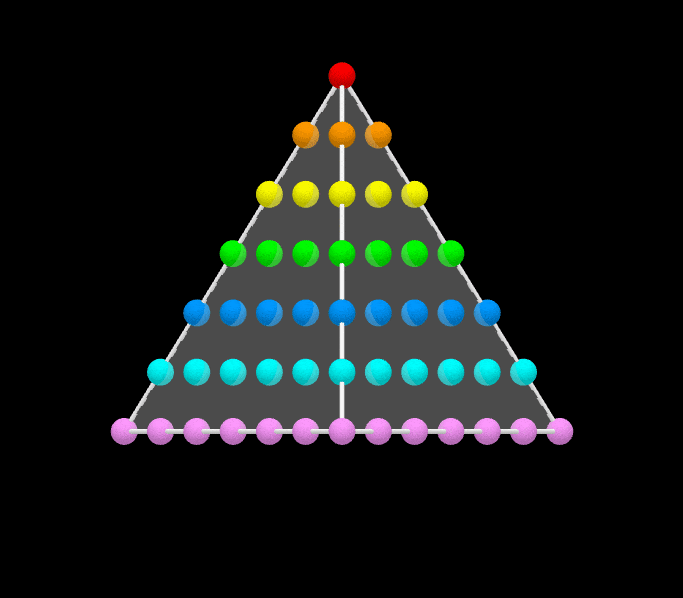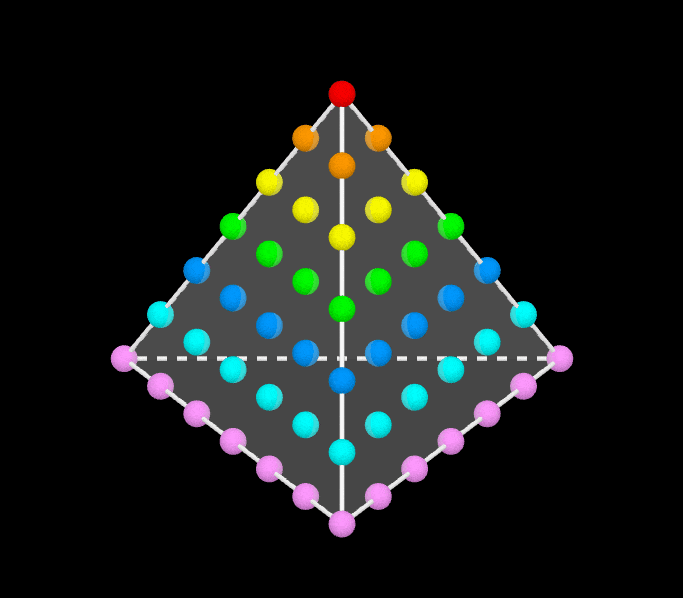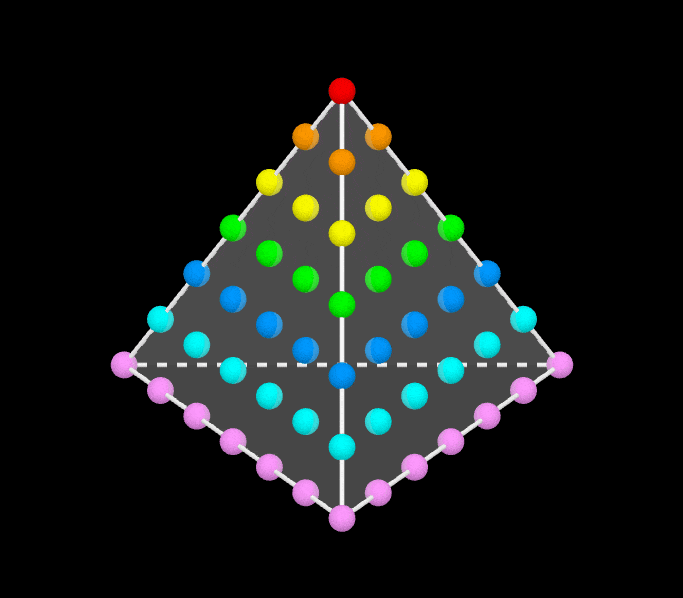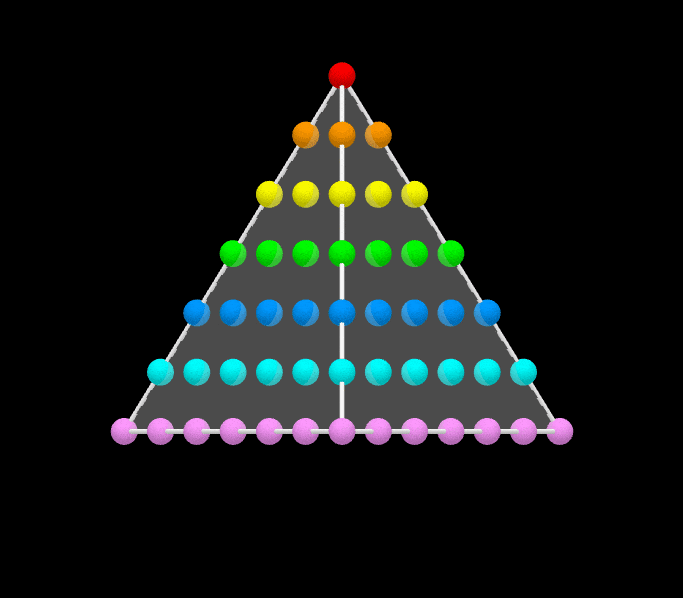
By Vincent Pantaloni, a wordless proof that the sum of the first n odd integers is n2.

By Vincent Pantaloni, a wordless proof that the sum of the first n odd integers is n2.
In 1620, the Grand Duke of Tuscany wrote to Galileo with a puzzling problem. In rolling three fair six-sided dice, it would seem that the sums 9 and 10 should appear with equal frequency, as there are six ways to produce each result:
10 = 6 + 3 + 1 = 6 + 2 + 2 = 5 + 4 + 1 = 5 + 3 + 2 = 4 + 4 + 2 = 4 + 3 + 3
9 = 6 + 2 + 1 = 5 + 3 + 1 = 5 + 2 + 2 = 4 + 4 + 1 = 4 + 3 + 2 = 3 + 3 + 3
But the duke had noticed that in practice 10 appears somewhat more often than 9. Why is this?
Galileo considered the problem and put his finger on the reason. What is it?
Next year’s date, 2025, is remarkable:
When asked his age, Augustus De Morgan used to say, “I was x years of age in the year x2.” (He was 43 in 1849.) People born in 1980 will be able to make the same cryptic response starting next year.
(Thanks to readers Chris Smith, Sam Householder, and Jim Howell.)
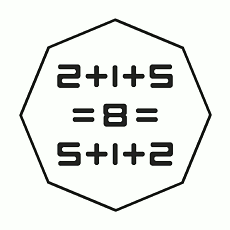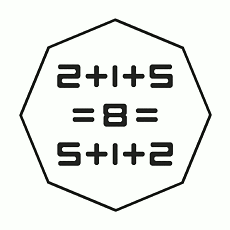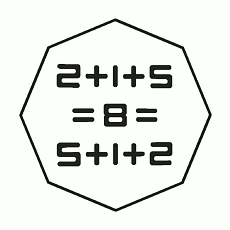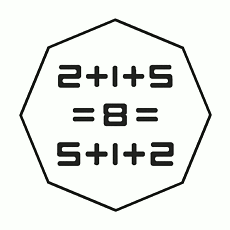
By Basile Morin, a very thorough demonstration of the commutativity of addition!
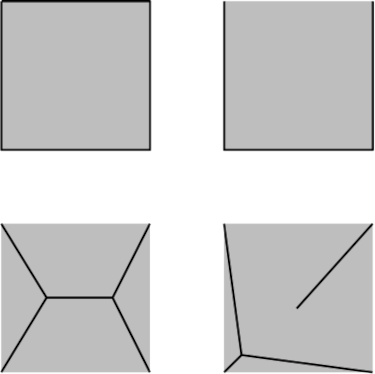
A creature living in the plane can’t see through a unit square — the square’s four line segments block its line of sight from any angle. Is there a way to achieve the same result using fewer building materials? Removing one of the square’s sides does the job — this requires only 3 units of line segment and still prevents anyone from seeing across the square’s area. The arrangement at lower left does better still, requiring only about 2.732 units. And the one at lower right requires only about 2.639 units.
Is that the shortest possible opaque set for the square? Possibly — but no one has been able to prove it.
Pekwachnamaykoskwaskwaypinwanik Lake is a lake in Manitoba. Its name is Cree for “where the wild trout are caught by fishing with hooks.”
Muckanaghederdauhaulia, a townland in County Galway, means “pig-marsh between two sea inlets.”
Saaranpaskantamasaari, an island in northeastern Finland, means “an island shat by Saara.”
Mamungkukumpurangkuntjunya is a hill in South Australia. Its name means “where the devil urinates.”
(Thanks, Colin.)
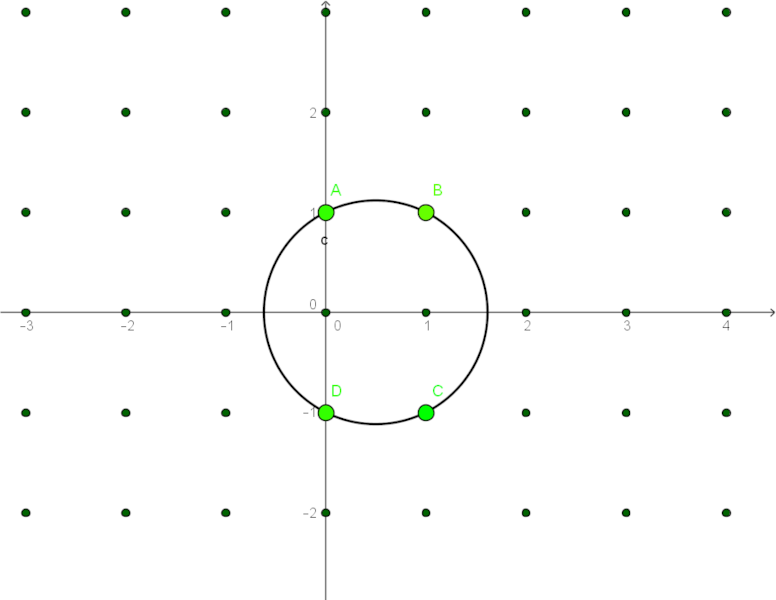
For any positive integer n, there exists a circle that passes through exactly n lattice points in the Euclidean plane.
This was first proven by Polish mathematician Andrzej Schinzel in 1958. It’s known as Schinzel’s theorem.
One of the most beautiful and moving of the bird-songs heard throughout the country which [French merchant Nicolas] Denys governed [in 17th-century Acadia], is that of the Veery, or Wilson’s Thrush. The Maliseet Indians of the Saint John River, as Mr. Tappan Adney has recently told us, say this bird is calling Ta-né-li-ain′, Ni-kó-la Dĕn′-i Dĕn′-i?, that is, ‘Where are you going, Nicolas Denys?’ and Mr. Adney thinks this an actual echo from the days of our author.
— From William Francis Ganong’s 1908 introduction to Denys’ Description and Natural History of the Coasts of North America, 1672