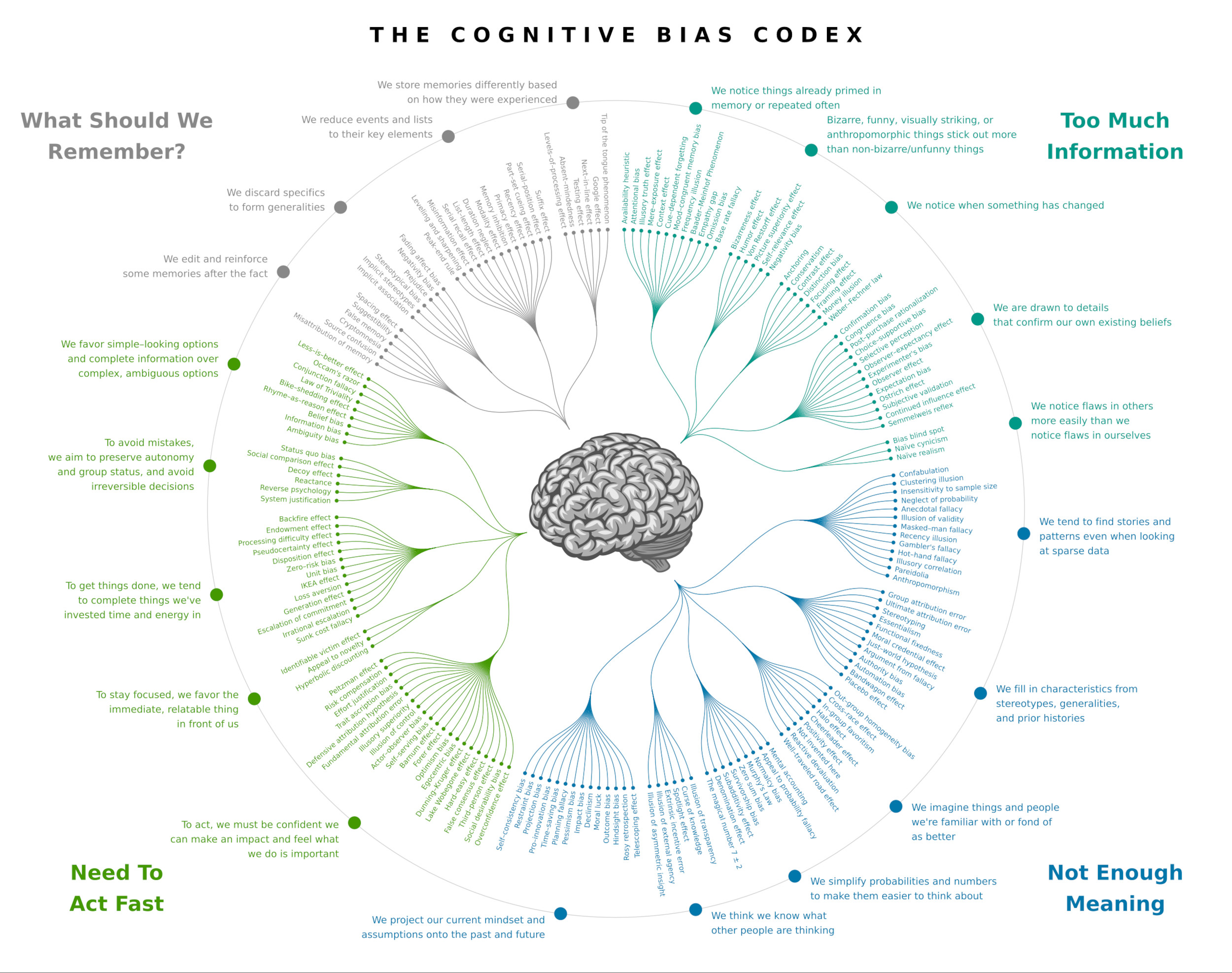
This is beautifully well done — a humiliating list of all the ways your brain can deceive you (click to enlarge).
Designed by John Manoogian III.

This is beautifully well done — a humiliating list of all the ways your brain can deceive you (click to enlarge).
Designed by John Manoogian III.

This is a picture of a cow. If you can’t see it (I couldn’t), there’s an explanatory image on page 66 of John McCrone’s 1991 book The Ape That Spoke.
The experience illustrates how the brain is able to construct a picture from limited data by relying on patterns and experience.

Steaming from New York to the Azores in 1867, Mark Twain noted a curious companion overhead:
We had the phenomenon of a full moon located just in the same spot in the heavens at the same hour every night. The reason of this singular conduct on the part of the moon did not occur to us at first, but it did afterward when we reflected that we were gaining about twenty minutes every day because we were going east so fast — we gained just about enough every day to keep along with the moon. It was becoming an old moon to the friends we had left behind us, but to us Joshuas it stood still in the same place and remained always the same.
(From The Innocents Abroad.)
02/11/2025 Reader Catalin Voinescu writes:
Mark Twain is talking absolute nonsense here.
The moon is in (almost) the same phase as seen from all over the world. It rises and sets at roughly the same local time, regardless of longitude, and the relation between phase and time of day when the moon is visible is the same everywhere (the full moon peaks at midnight; a week later, the last-quarter moon rises around midnight, peaks in the morning and sets around noon; and so on).
Even ignoring moon phase and local time, the moon rises, peaks and sets almost 50 minutes later every day, so gaining 20 minutes every day would not be enough.
(Thanks, Catalin.)
(Until William Herschel’s advances in telescopes, stars seemed to have “rays” or “tails.”)
At a dinner given by Mr Aubert in the year 1786, William Herschel was seated next to Mr Cavendish, who was reputed to be the most taciturn of men. Some time passed without his uttering a word, then he suddenly turned to his neighbour and said: ‘I am told that you see the stars round, Dr Herschel’. ‘Round as a button’, was the reply. A long silence ensued till, towards the end of the dinner, Cavendish again opened his lips to say in a doubtful voice: ‘Round as a button?’ ‘Exactly, round as a button’, repeated Herschel, and so the conversation ended.
— Constange A. Lubbock, The Herschel Chronicle, 1933
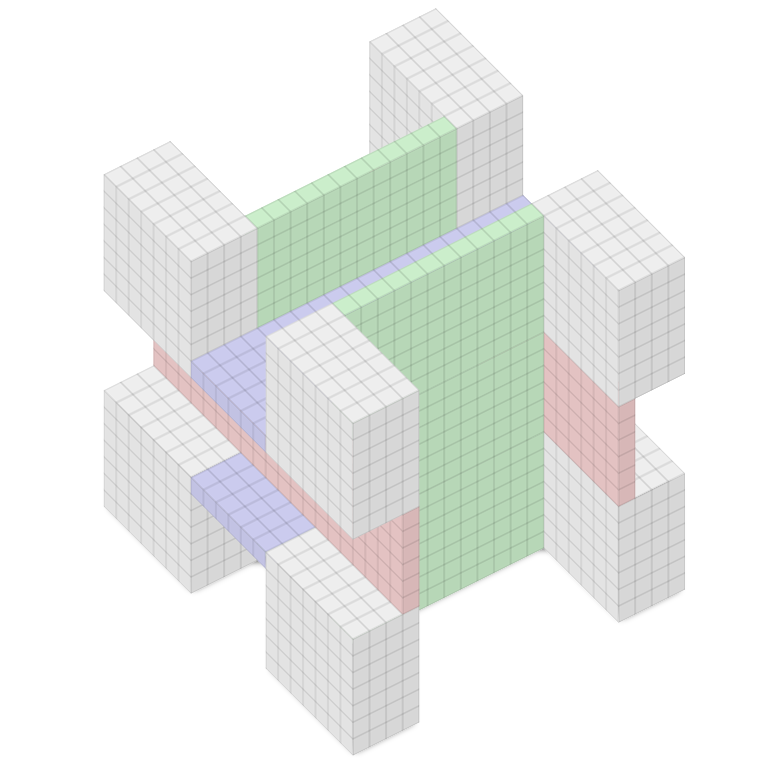
An art gallery with n walls will always be safe with n/3 guards — the guards will always be able arrange themselves to observe the whole gallery.
That’s Chvátal’s art gallery theorem, discovered in 1973 by mathematician Václav Chvátal. Interestingly, it’s true only of two-dimensional floor plans — a three-dimensional gallery may not be safe even if you post a guard at every corner.
Take a 20 × 20 × 20 cube and remove a 12 × 6 channel from the front and back faces; a 6 × 3 channel from the left and right faces; and a 6 × 6 channel from the top and bottom faces, as shown. The result is the Octoplex, eight 4 × 7 × 7 theaters connected to each other and to a central lobby by passages 1 unit wide.
Remarkably, even if we mount a camera at every one of this figure’s 56 corners, there will remain a small region in the central lobby that no camera can see.
(T.S. Michael, “Guards, Galleries, Fortresses, and the Octoplex,” College Mathematics Journal 42:3 [May 2011], 191-200.)

Song of a neighborhood nightingale transcribed in 1868 by German naturalist Johann Matthäus Bechstein:
Tioû, tioû, tioû, tioû.
Spe, tiou, squa.
Tiô, tiô, tiô, tiô, tio, tio, tio, tix.
Coutio, coutio, coutio, coutio.
Squô, squô, squô, squô.
Tzu, tzu, tzu, tzu, tzu, tzu, tzu, tzu, tzu, tzi.
Corror, tiou, squa pipiqui.
Zozozozozozozozozozozozo, zirrhading!
Tsissisi, tsissisisisisisisis.
Dzorre, dzorre, dzorre, dzorre, hi.
Tzatu, tzatu, tzatu, tzatu, tzatu, tzatu, tzatu, dzi.
Dlo, dlo, dlo, dlo, dlo, dlo, dlo, dlo, dlo.
Quio, tr rrrrrrrr itz.
Lu, lu, lu, lu, ly, ly, ly, liê, liê, liê, liê.
Quio, didl, li lulylie.
Hagurr, gurr quipio!
Coui, coui, coui, coui, qui, qui, qui, qui, gai, gui, gui, gui.
Goll goll goll goll guia hadadoi.
Couigui, horr, he diadia dill si!
Hezezezezezezezezezezezezezezezeze couar ho dze hoi.
Quia, quia, quia, quia, quia, quia, quia, quia, ti.
Ki, ki, ki, ïo, ïo, ïo, ioioioio ki.
Lu ly li le lai la leu lo, didl ïo quia.
Kigaigaigaigaigaigaigai guiagaigaigai couior dzio dzio pi.
In his 1795 Natural History of Cage Birds, he notes that some captive birds “never sing unless confined within narrow limits, being obliged, as it would appear, to solace themselves, for the want of liberty, with their song,” and so should never be given freedom within a room.
See Bird Talk, Bird Songs, and Who’s Who.
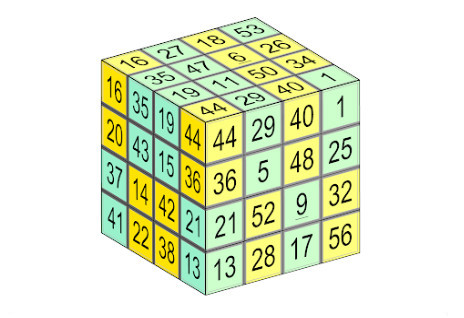
Reader William Walkington devised this “hollow” cube of order 4, each of whose faces is a magic square that draws on numbers from 1 to 56. The lines of four numbers in each row, column, long diagonal, and even some of the broken diagonals, produce the magic sum 114. Further, remarkably, when the figure is “scrambled” like a Rubik’s cube, the result is often another magic box cube:
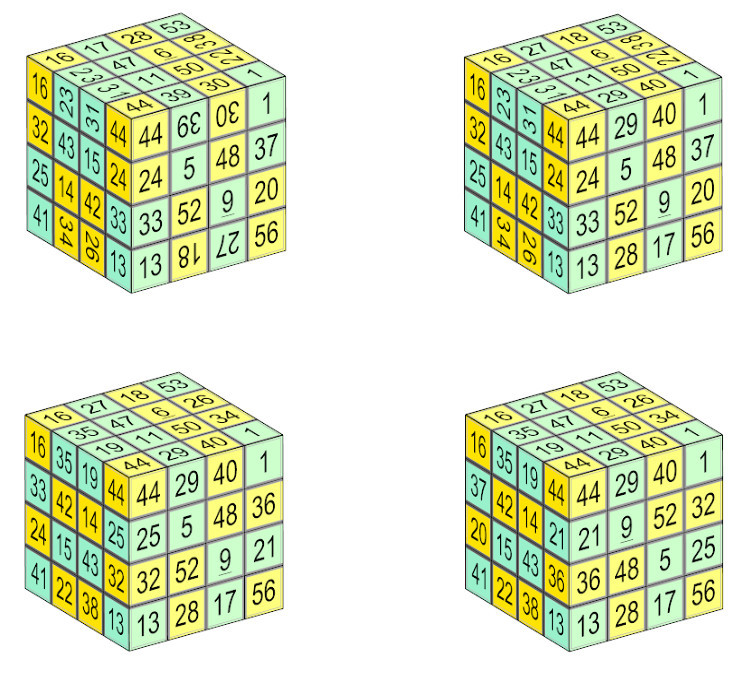
For more information, see his site. (Thanks, William.)

Lord David Cecil called Samuel Johnson “an outstanding example of the charm that comes from an unexpected combination of qualities. In general, odd people are not sensible and sensible people are not odd. Johnson was both and often both at the same time.”