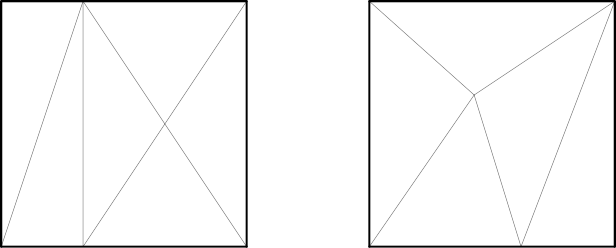
A square can be divided into an even number of triangles of equal area — but not into an odd number.

A square can be divided into an even number of triangles of equal area — but not into an odd number.
Every unjust act is inexpedient;
No unjust act is expedient;
No expedient act is unjust;
Therefore every expedient act is just.
— Ralph L. Woods, How to Torture Your Mind, 1969
I just found this in a 1950 issue of Pi Mu Epsilon Journal:
Question: How many legs has a horse?
Answer: Twelve; two in front, two behind, two on each side, and one in each corner.
Later in the same volume, Marlow Sholander shows that in fact every horse has an infinite number of legs.
That’s to say nothing of color. And see Chasing Leo.
Suppose your dog eats the ace of spades and you’re forced to play poker with a 51-card deck. Does this make it more or less likely that you’ll be dealt a two-pair hand?
The answer is not immediately clear. The loss of the ace means that fewer two-pair hands are possible, but the total universe of possible five-card hands is also reduced.
Surprisingly, the probability is unchanged. “[T]he probability of getting a Two-Pair hand in the 51-card deck with the missing Ace of Spades is exactly the same as for a 52-card standard deck,” notes George Mason University mathematician D.M. Anderson. And “[i]t turns out that this seemingly magical result for a deck with a missing Ace of Spades is not limited to Two-Pair hands. Indeed, examining the traditional hierarchy of 5-card poker hands, we find an analogous result holds for One-Pair hands, Three-of-a-Kind, Full Houses and Four-of-a-Kind.”
(D.M. Anderson et al., “Not Playing With a Full Deck?”, Recreational Mathematics Magazine 11:18 [March 2024], 51-63.)
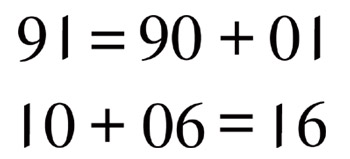
A doubly true equation by Basile Morin.
This remarkable phenomenon was discovered by Cambridge mathematician James Grime. Number five six-sided dice as follows:
A: 2, 2, 2, 7, 7, 7
B: 1, 1, 6, 6, 6, 6
C: 0, 5, 5, 5, 5, 5
D: 4, 4, 4, 4, 4, 9
E: 3, 3, 3, 3, 8, 8
Now, on average:
A beats B beats C beats D beats E beats A
and
A beats C beats E beats B beats D beats A.
Interestingly, though, if each die is rolled twice rather than once, then the first of the two chains above remains unchanged except that D now beats C — and the second chain is reversed:
A beats D beats B beats E beats C beats A.
As a result, if each of two opponents chooses one of the five dice, a third opponent can always find a remaining die that beats them both (so long as he’s allowed to choose whether the dice will be rolled once or twice).
(Ward Heilman and Nicholas Pasciuto, “What Nontransitive Dice Exist Among Us?,” Math Horizons 24:4 [April 2017], 14-17.)
From Pi Mu Epsilon Journal, November 1950:
(1/2)3 < (1/2)2.
Taking the logarithm to the base 1/2 of each member of the above inequality, we write
3 log1/2(1/2) < 2 log1/2(1/2).
But logbb = 1. Therefore
3 < 2.

Several claimants have been put forth as the originators of the modern tropical cyclone ‘naming’ system. Australian weather meteorologist, Clement L. Wragge, is one of the best-established holders of the title. … Most ingeniously, he gained a measure of personal revenge by christening some of the nastiest storms with politicians’ names such as Drake, Barton, and Deakin. Modern hurricane researcher Chris Landsea noted that, by using such a personal naming system, Wragge could publicly describe a politician (say one who was less than generous with weather-bureau appropriations) as ‘causing great distress’ or ‘wandering aimlessly about the Pacific.’
— Randy Cerveny, Freaks of the Storm, 2006