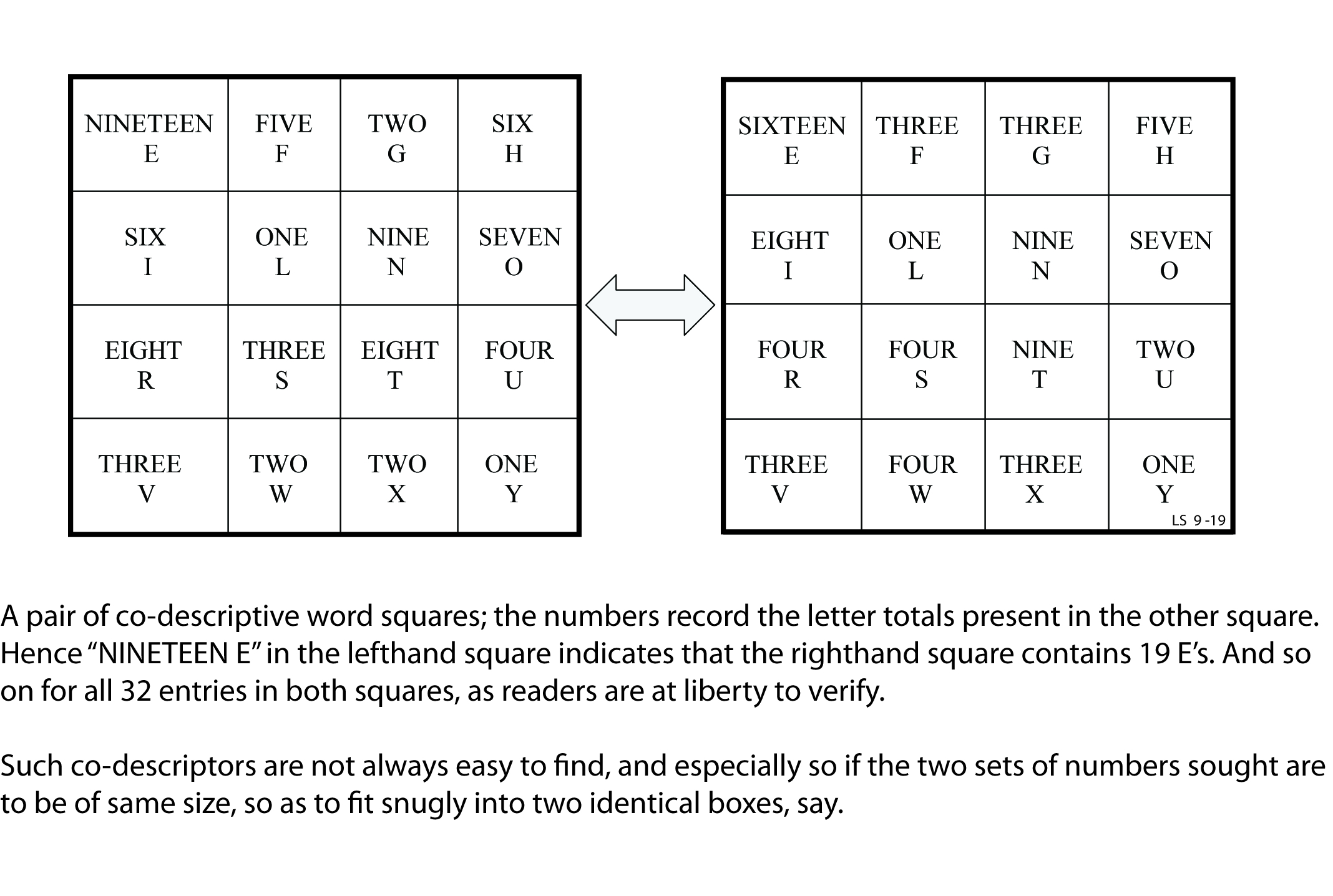
Suppose your dog eats the ace of spades and you’re forced to play poker with a 51-card deck. Does this make it more or less likely that you’ll be dealt a two-pair hand?
The answer is not immediately clear. The loss of the ace means that fewer two-pair hands are possible, but the total universe of possible five-card hands is also reduced.
Surprisingly, the probability is unchanged. “[T]he probability of getting a Two-Pair hand in the 51-card deck with the missing Ace of Spades is exactly the same as for a 52-card standard deck,” notes George Mason University mathematician D.M. Anderson. And “[i]t turns out that this seemingly magical result for a deck with a missing Ace of Spades is not limited to Two-Pair hands. Indeed, examining the traditional hierarchy of 5-card poker hands, we find an analogous result holds for One-Pair hands, Three-of-a-Kind, Full Houses and Four-of-a-Kind.”
(D.M. Anderson et al., “Not Playing With a Full Deck?”, Recreational Mathematics Magazine 11:18 [March 2024], 51-63.)